Д. Елиусизов
Есеп №1. Кел келген натурал сан үшін, келесі тұжырымды дәлелдеңіздер: осы санның барлық натурал бөлгіштерін, кез келген екі көрші тұрған бөлгіштердің біреуі екіншісіне бөлінетіндей, шеңбер бойымен қойып шығуға болады. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №2. Натурал $N$ санының $k$ натурал бөлгіші бар. Сол санның барлық натурал бөлгіштерін, кез келген $1\le i < k$ үшін, $d_i/d_{i+1}$ немесе $d_{i+1}/d_i$ саны жай болатындай, $d_1$, $\ldots$, $d_k$ тізбегіне тізіп шығуға болатынын дәлелдеңіздер. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
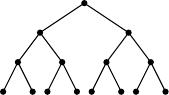
Есеп №3. Пирамида түріндегі $n+1$ деңгейлі толық ағаш берілген. Түбір (1-ші деңгей) мен ең соңғы ($(n+1)$-ші) деңгейдегі нүктелерден басқа қалған деңгейлердегі әр нүктеден төмен қарай екі қабырға шығады, және төбеден бір қабырға кіреді. 1-ші суретте мысал $n = 3$ үшін көрсетілген. Әрбір түс үшін бірдей түске боялған барлық қабырғалар қандай да бір деңгейдегі төбеден ең төменгі деңгейдегі төбеге дейін жол құрайтындай, ағашты берілген әртүрлі $2^n$ түске (әр қабырға бір ғана түске боялған) қанша әдіспен бояуға болады? (Келесі төбе алдыңғы төбемен қабырғамен қосылған және деңгейі сол төбеден төмен жататын төбелер тізбегін жол деп атаймыз.)
комментарий/решение(3) олимпиада
Есеп №4. Өлшемі $2^n \times 2^n$ ($n \ge 3$) болатын тақтадан бір шаршыны қиып алып тастаған. Қалған тақтаны үш шаршыдан құралған бұрыш фигуралармен толығымен жауып шығудың әдіс саны $3^{{4^{n-3}}}$-тен кем емес екенін дәлелде. (Ешқандай бұрыштар бір-бірін жаппайды). ( Д. Елиусизов )
комментарий/решение олимпиада
Есеп №5. Өлшемі $2^n \times 2^n$ ($n \ge 3$) болатын тақтадан бір шаршыны қиып алып тастаған. Қалған тақтаны үш шаршыдан құралған бұрыш фигуралармен толығымен жауып шығудың әдіс саны $4^{3 \cdot 4^{n-3}}$- тен кем емес екенін дәлелде. (Ешқандай бұрыштар бір-бірін жаппайды.) ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №6. Екі тасбақа бір уақытта координатасы $(0, 0)$ нүктеден шығып, әр жүрісте бір уақытта бір бүтін координатаға оңға немесе жоғары қарай жүреді (яғни $\left( {x,y} \right)$ нүктесінен $\left( {x + 1,y} \right)$ немесе $\left( {x,y+1} \right)$ нүктесіне). Егер тасбақалар соңғы рет $\left( {0,0} \right)$ нүктесінде кездескен болса, олар $\left( {n,n} \right)$ нүктесіне қанша әдіспен жете алады? ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №7. Екі тасбақа бір уақытта координатасы $(0, 0)$ нүктеден шығып, әр жүрісте бір уақытта бір бүтін координатаға оңға немесе жоғары қарай жүреді (яғни $\left( {x,y} \right)$ нүктесінен $\left( {x + 1,y} \right)$ немесе $\left( {x,y+1} \right)$ нүктесіне). Егер тасбақалар соңғы рет $\left( {0,0} \right)$ нүктесінде кездескен болса, олар $\left( {n,n} \right)$ нүктесіне қанша әдіспен жете алады? ( Д. Елиусизов )
комментарий/решение(3) олимпиада
Есеп №8. $A = \{1, 2, \ldots, n\}$ жиыны және $m$ натурал саны берілсін. Егер $a < b$ сандары бір бөлікте, $c < d$ сандары басқа бөлікте болса, $(a-d)(b-c) > 0$ болатындай $A$ жиынын $m$ бөлікке неше тәсілмен бөлсе болады?
Мысалға, егер $n = 4$, $m = 2$ болса, онда $A = \{1, 2, \ldots, 4\}$ жиынын 5 тәсілмен бөлсе болады: $$ \{1, 2\} \{3, 4\}; \quad \{1, 2, 3\} \{4\}; \quad \{1, 2, 4\} \{3\}; \quad \{1, 3, 4\} \{2\}; \quad \{2, 3, 4\} \{1\}. $$ ( Д. Елиусизов )
комментарий/решение(3) олимпиада
Есеп №9. Әрбір торкөзіне 0 немесе 1 жазылған шаршы кестені бинарлық деп атаймыз. Егер бинарлық кестенің әрбір жолында және әрбір бағанында дәл 2 бірлік жазылған болса, ол регулярлы деп аталады. Өлшемі $n\times n$ ($n > 1$ — бір бекітілген натурал сан) болатын әртүрлі регулярлы кестелердің санын анықта. (Кестенің жолдары мен бағандары нөмірленген деп есептеуге болады: тек бұру, шағылыстыру т.с.с. жолмен беттесетін кестелер әртүрлі деп есептеледі.) ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №10. Тақ, натурал $m > 1,k$ сандары және $p > mk+1$ болатын $p$ жай саны берілген. Келесі тұжырымды дәлелде: ${{(C_{k}^{k})}^{m}}+{{(C_{k+1}^{k})}^{m}}+\ldots +{{(C_{p-1}^{k})}^{m}}$ қосындысы ${{p}^{2}}$ санына бөлінеді. Мұнда $C_{n}^{k}=\frac{n!}{k!(n-k)!}$ — биномиалдық коэффициент. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №11. Кез келген нақты $a_1, a_2, \ldots, a_n$, $b_1, b_2, \ldots, b_n$ оң сандары үшін келесі теңсіздік орындалатынын дәлелдеңдер: $$(a_1^{2010} + a_2^{2010} + \ldots + a_n^{2010})(b_1^{2010} + b_2^{2010} + \ldots + b_n^{2010}) \ge $$ $$\ge (a_1b_1^{2009} + a_2b_2^{2009} + \ldots + a_nb_n^{2009})(a_1^{2009}b_1 + a_2^{2009}b_2 + \ldots + a_n^{2009}b_n).$$ ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №12. $\{a_n\}_{n \ge 1}$ тізбегі былайша анықталған: $$a_1 = \alpha \text{ және } n \ge 1 \text{ үшін } a_{n+1} = 2 a_n^2 - 1.$$ Егер $a_{2010} = 0$ болса, $\alpha$ саны қанша әртүрлі нақты мән қабылдай алады? ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №13. $ABC$ үшбұрышы берілген. $C$ нүктесі арқылы өтетін, фокустары $A$ және $B$ нүктелері болатын $\Omega_1$ эллипсін қарастырайық. Осыған ұқсас $\Omega_2, \Omega_3$ (фокустары сәйкесінше $B, C$ және $C, A$) эллипстерін анықтаймыз. Егер осы үш эллипстің ортақ $D$ нүктесі бар болса, онда $A, B, C, D$ нүктелерінің бір шеңбердің бойында жататынын дәлелдеңдер (фокустары деп аталатын бекітілген екі нүктеге дейінгі қашықтықтарының қосындысы тұрақты мәнге тең болатын нүктелердің геометриялық орны эллипс деп аталады). ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №14. Кез келген $0 < {{a}_{1}}\le {{a}_{2}}\le \ldots \le {{a}_{n}}$ ($n\ge 3$) сандары үшін $\dfrac{a_{1}^{2}}{{{a}_{2}}}+\dfrac{a_{2}^{3}}{a_{3}^{2}}+\ldots +\dfrac{a_{n}^{n+1}}{a_{1}^{n}}\ge {{a}_{1}}+{{a}_{2}}+\ldots +{{a}_{n}}$ теңсіздігі орындалатынын дәлелдеңіз. ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Есеп №15. Әрбір натурал $k$ саны үшін ${{F}_{k}}$ арқылы дәл $k$ бірлік шаршыдан тұратын байланысты жазық фигуралардың жиынын белгілейік. Кез келген $f$ жазық фигурасы үшін $S\left( f \right)$ арқылы оны қамти алатын тіктөртбұрыштың ауданының ең аз мүмкін мәнін белгігейік. Берілген натурал $n$ үшін $\underset{f\in {{F}_{n}}}{\mathop{\max }}\,S\left( f \right)$ мәнін анықта. ( Д. Елиусизов )
комментарий/решение олимпиада
Есеп №16. $f:\mathbb{R}\to \mathbb{R}$ функциясы, мұндағы $\mathbb{R}$ — нақты сандар өрісі, кез келген $x,y\in \mathbb{R}$ үшін $f(f(x)+x+y)=2x+f(y)$ тепе-теңдігін қанағаттандырады. Онда мынадай екі ${{\alpha }_{1}},{{\alpha }_{2}}\in \mathbb{R}$ сандары табылатынын дәлелдеңіздер: әрбір $r$ нақты саны дәл бір ғана әдіспен $r={{r}_{1}}+{{r}_{2}}$ қосындысына жіктеледі, мұнда әрбір $i=1,2$ үшін ${{r}_{i}}\in \mathbb{R}$ және $f({{r}_{i}})={{\alpha }_{i}}\cdot {{r}_{i}}$. ( Д. Елиусизов, Е. Байсалов )
комментарий/решение(3) олимпиада
Есеп №17. Егер $a+b+c+2=abc$ екені белгілі болса, оң нақты $a,b,c$ сандары үшін $ab+bc+ca\ge 2(a+b+c)$ теңсіздігін дәлелдеңіздер. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №18. Кез келген $x,y\in \mathbb{R}$ үшін $f(xy+f(x))=xf(y)+f(x)$ тепе-теңдігін қанағаттандыратын барлық $f:\mathbb{R}\to \mathbb{R}$ функциясын табыңыздар, мұндағы $\mathbb{R}$ — нақты сандар жиыны. ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Есеп №19. Егер $a+b+c+2=abc$ екені белгілі болса, оң нақты $a,b,c$ сандары үшін $ab+bc+ca\ge 2(a+b+c)$ теңсіздігін дәлелдеңіздер. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №20. $P(n)$ саны, ол $n$ санын екінің дәрежелерінің қосындысы түрінде келтіру саны болсын (қосылғыштардың орын ауысып тұруы маңызды емес). Мысалға, $P(5) = 4$, өйткені $5=4+1=2+2+1=2+1+1+1=1+1+1+1+1$.
Егер $a_k$ саны, ол $k$ санының екілік жүйедегі бірліктер саны болса, онда кез келген натурал $n$ саны үшін $$P(n) + (-1)^{a_1} P(n-1) + (-1)^{a_2} P(n-2) + \ldots + (-1)^{a_{n-1}} P(1) + (-1)^{a_n} = 0$$ теңдігінің орындалатынын дәлелдеңіздер. ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Есеп №21. Өлшемі $4\times 4$ болатын кестенің жолдары 1, 2, 3, 4 сандарымен, ал бағандары $a$, $b$, $c$, $d$ әріптерімен белгіленген және оның әрбір торкөзіне 0 немесе 1 жазылған. Егер осы кестенің әрбір жолында және әрбір бағанында дәл екі бірлік жазылған болса, оны жарамды деп атаймыз. Жарамды кестелердің санын анықтаңдар. ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Есеп №22. $abc\le 1$ шартын қанағаттандыратын кез келген оң нақты $a$, $b$, $c$ сандары үшін $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge 1+\frac{6}{a+b+c}$. теңсіздігін дәлелдеңіз. ( Д. Елиусизов )
комментарий/решение(13) олимпиада
Есеп №23. Мынадай шартты қанағаттандыратын барлық коэффициенттері нақты $P(x)$ көпмүшеліктерді анықта: әрбір рационал $r$ саны үшін $P(x)=r$ теңдеуінің рационал шешімі табылады. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №24. $2n$ төбесі және ${2n(n-1)}$ қабырғасы бар (ориентацияланбаған, тұзақсыз) граф берілген. Әрбір қызыл төбеден дәл $n$ қызыл қабырға шығатындай етіп осы графтың кейбір төбелері мен қабырғаларын қызыл түске бояуға болатынын дәлелдеңдер. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №25. ${{A}_{0}}$, ${{B}_{0}}$, ${{C}_{0}}$ нүктелері — $ABC$ үшбұрышының сәйкесінше $BC$, $CA$, $AB$ қабырғаларының ортасы, ал ${{A}_{1}}$, ${{B}_{1}}$, ${{C}_{1}}$ нүктелері — сәйкесінше $BAC$, $CBA$, $BCA$ қисықтарының (ұзындық бойынша) ортасы. Онда ${{A}_{0}}{{A}_{1}}$, ${{B}_{0}}{{B}_{1}}$, ${{C}_{0}}{{C}_{1}}$ түзулерінің бір нүктеде қиылысатынын дәлелде. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №26. Кез келген оң нақты $a,b,c$ сандары үшін ${{a}^{3}}+{{b}^{3}}+{{c}^{3}}-3abc\ge M(|a-b{{|}^{3}}+|b-c{{|}^{3}}+|c-a{{|}^{3}})$ теңсіздігі орындалатындай нақты $M$ санының ең үлкен мәнін тап. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №27. $ABC$ үшбұрышына іштей сызылған $\omega $ шеңбері $BC$ қабырғасын $K$ нүктесінде жанайды. $B$ мен $C$ нүктелері арқылы өтетін және $\omega $ шеңберін $S$ нүктесінде жанайтын шеңбер жүргізейік. $SK$ түзуі $ABC$ үшбұрышына сыртта іштей сызылған және $BC$ қабырғасын жанайтын шеңбердің центрі арқылы өтетінін дәлелде. ( Д. Елиусизов )
комментарий/решение олимпиада
Есеп №28. $a_1, a_2, \dots, a_n$ бүтін сандар тізбегі арифметикалық прогрессия құрайды, және кез келген $i=1, 2, \dots , n-1$ үшін $a_n$ саны $i$ санына бөлінеді де, және де сол $a_n$ саны $n$ санына бөлінбейді. $n$ санының жай санның дәрежесі екенін дәлелдеңіздер. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №29. Нақты $x, y, z \in (0;1)$ сандары үшін $8xyz = (1 - x)(1 - y)(1 - z)$ теңдігі орындалады. $x+y+z \geq 1$ теңсіздігін дәлелдеңіздер. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №30. Шегіртке координат өсіндегі 0 нүктеде тұр. Әр секірім сайын оған координатасы $x$ болатын нүктеден координатасы $x + 1$ немесе $2x$ болатын нүктеге секіру рұқсат. Координаттың «салмағы» деп, сол координатаға жетуге қажет секірім санының ең кішісін айтамыз. Координатасы $x < 2010$ болатын ең үлкен салмақты табыңыздар. ( Д. Елиусизов )
комментарий/решение олимпиада
Есеп №31. $N = 10^{10}-1$ болсын. $\{|{{a}_{1}}-{{a}_{2}}|, |{{a}_{2}}-{{a}_{3}}|, |{{a}_{3}}-{{a}_{4}}|,\dots, |{{a}_{N-1}}-{{a}_{N}}|\}=\{1,10,{{10}^{2}}, {{10}^{3}},\dots, {{10}^{9}}\}$ болатындай $(1,2,\ldots ,N)$ сандарының қандай да бір $({{a}_{1}},{{a}_{2}},\ldots ,{{a}_{N}})$ ауыстырылымы бар екенін дәлелдеңдер (қандай да бір $\,|{{a}_{i}}-{{a}_{i+1}}|$ алымы қайталанып келуі мүмкін, бірақ та $({{a}_{1}},{{a}_{2}},\ldots ,{{a}_{N}})$ жиынының барлық мүшелері сол алымдардын ішінде кездесу керек). ( Д. Елиусизов )
комментарий/решение олимпиада
Есеп №32. $A_n$ арқылы 1, 2, $\dots$, $n$ тізбегін келесі шартты қанағаттандыратын ішкі тізбекке бөлу жиынын белгілейік: сол ішкі тізбектің кез келген екі көрші сандар жұптығы бірдей. Ал $B_n$ арқылы 1, 2, $\dots$, $n$ тізбегін келесі шартты қанағаттандыратын ішкі тізбекке бөлу жиынын белгілейік: сол ішкі тізбектің кез келген екі көрші сандар жұптығы әртүрлі. Мысалға, $\{(1, 4, 5, 8), (2, 3), (6, 9), (7)\}$ жиындары $A_9$ жиынының элменттері, ал $\{(1, 3, 5), (2, 4), (6)\}$ жиындары $B_6$ жиынының элементтері. Кез келген натурал $n$ саны үшін $A_n$ және $B_{n+1}$ жиындарында элементтер саны тең екенін дәлелдеңіз. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №33. $n$ натурал саны берілген. Теңсіздікті дәлелде: $\sum\limits_{i=1}^{n}{\frac{1}{i(i+1)(i+2)(i+3)(i+4)}} < \frac{1}{96}$. ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Есеп №34. Егер натурал санның цифрларын қандай ретпен ауыстырып жазсақ та жай сан алсақ, онда оны абсолют жай деп атаймыз. Мысалы, 113 абсолют жай сан (113, 131, 311 – бәрі жай сандар). Ондық жазылуында 1, 3, 7, 9 цифрінің бәрі кездесетін абсолют жай сан табылмайтынын дәлелде. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №35. $({{2}^{m}}+{{1,2}^{n}}+1)={{2}^{(m,n)}}+1$ шартын қанағаттандыратын барлық натурал $(m; n)$ жұптарын табыңыздар. Бұл жерде $(a,b)$ — натурал $a$ және $b$ сандарының ең үлкен ортақ бөлгіші. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №36. Кез келген оң нақты $x$ үшін $f(f(x))=\alpha f(x)-\beta x$ тепе-теңдігін қанағаттандыратын $f:\left( 0,+\infty \right)\to \left( 0,+\infty \right)$ функциясы табылатын барлық $\left( \alpha ,\beta \right)$ оң нақты сандар жұптарын анықта. ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №37. Кез келген $p$ жай саны үшін саны $({x^2} + p{t^2})({y^2} + p{t^2})({z^2} + p{t^2})$ толық квадрат болатындай шексіз көп $(x, y, z, t)$ өзара тең емес бүтін сандардың төрттіктері табылатынын дәлелдеңіз. ( Д. Елиусизов, Е. Байсалов )
комментарий/решение(1) олимпиада
Есеп №38. Дано натуральное число $m\geq2.$ Последовательность натуральных чисел $(b_0,b_1,\ldots,b_m)$ назовем вогнутой, если $b_k+b_{k-2}\le2b_{k-1}$ для всех $2\le k\le m.$ Докажите, что существует не более $2^m$ вогнутых последовательностей, начинающихся с $b_0=1$ и $b_1=2.$ ( Д. Елиусизов )
комментарий/решение(1) олимпиада
Есеп №39. Докажите, что существует по крайней мере $100!$ способов разбить число $100!$ на сумму слагаемых из множества $\{1!, 2!, 3!, \ldots, 99! \}$. (Разбиения, отличающиеся порядком слагаемых, считаются одинаковыми; любое слагаемое можно использовать несколько раз. Напомним, что $n!=1 \cdot 2 \cdot \ldots \cdot n.$) ( Д. Елиусизов )
комментарий/решение(2) олимпиада
Есеп №40. $\{a_n\}$ тізбегі келесідей анықталған: $a_0=1$ және $n \ge 1$ үшін ${a_n} = \sum\limits_{k = 1}^{[\sqrt n ]} {{a_{n - {k^2}}}}$. $a_1,a_2,\ldots,a_{10^6}$ сандарының арасында кемінде 500 жұп сан бар екенін дәлелдеңіз. (Бұл жерде $[x]$ арқылы $x$ санынан аспайтын ең үлкен бүтін санды белгілейміз.) ( Д. Елиусизов )
комментарий/решение(2) олимпиада