Республиканская олимпиада по математике, 2012 год, 9 класс

Даны две окружности $k_1$ и $k_2$ с центрами в точках $O_1$ и $O_2$ которые пересекаются в точках $A$ и $B$. Через точку $A$ проходит две прямые которые пересекают окружность $k_1$ в точках $N_1$ и $M_1$, а окружность $k_2$ в точках $N_2$ и $M_2$ (точки $A$, $N_1$ и $N_2$ лежат на одной прямой). Обозначим середины отрезков $N_1N_2$ и $M_1M_2$ через $N$ и $M$. Доказать, что:
а) точки $M$, $N$, $A$ и $B$ лежат на одной окружности.
б) центр окружности проходящий через $M$, $N$, $A$ и $B$ лежит на середине отрезка $O_1O_2$.

Комментарий/решение

a) $\angle BM_{2}A = \angle BN_{2}A$ и $\angle AN_{1}B = \angle AM_{1}B$ откуда следует что треугольники $BN_{1}N_{2}, \ BM_{1}M_{2}$ подобны или $\dfrac{BM_{1}}{BN_{1}} = \dfrac{BM}{BN}$ и треугольники $BMM_{1}, \ BNN_{1}$ так же подобны по углу и пропорциональности отношений сторон, получаем $\angle ANB = \angle AMB$.

Значит точки $M,N,A,B$ лежат на одной окружности $\omega$.

б) Пусть имеется две концентрические окружности с центрам в точке $O_{1}$ и радиусами $r_{1},r_{2}$ и $r_{1}<r_{2}$.

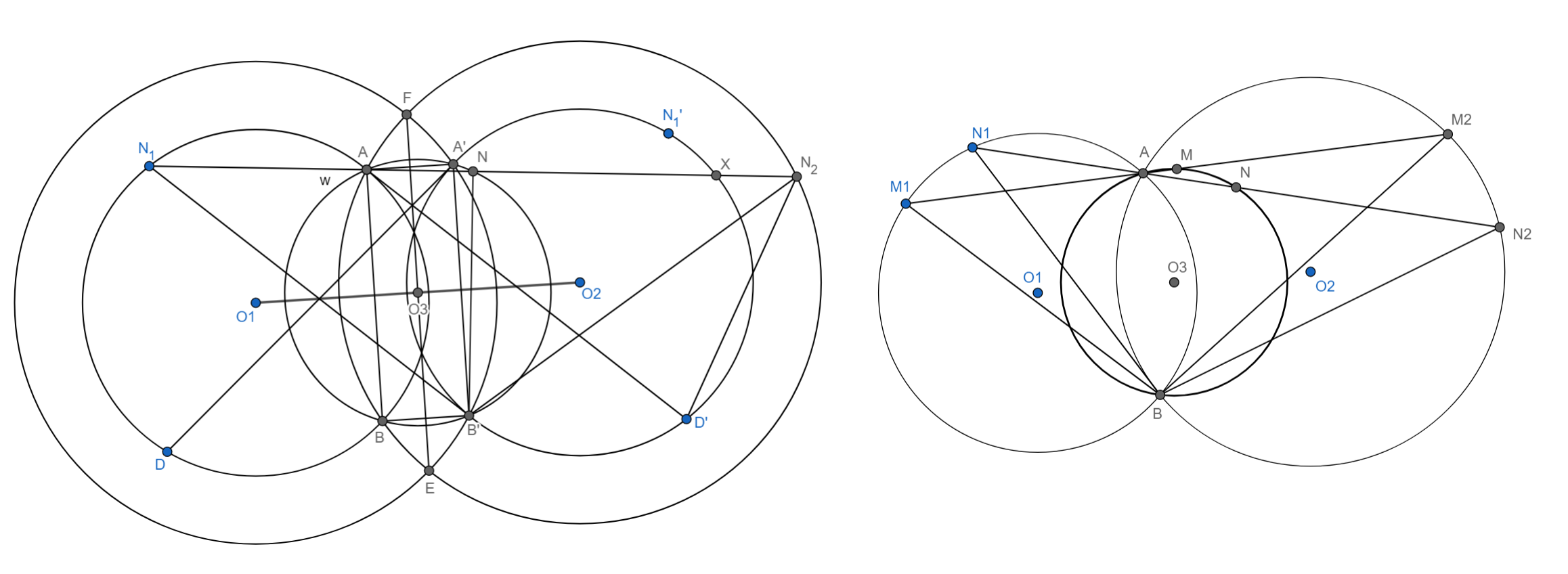
1)Пусть имеется аналогичные окружности. но центром в точке $O_{2}$ с теми же радиусами, положим что окружности с радиусами $r_{2}$ пересекаются в точках $F,E$, а окружность с центром $O_{1}$ и с радиусом $r_{1}$ с окружность с центром в $O_{2}$ и $r_{2}$ в точках $A,B$. Тогда две другие в симметричных относительно $FE$ точках $A',B'$.

2) Возьмем на окружности $(O_{1},r_{1})$ произвольную точку $N_{1}$ проведем $N_{1}A$ пусть она пересекает $(O_{2},r_{1})$ и $(O_{2},r_{2})$ в соответственных точках $X,N_{2}$ и докажем что $N_{2}B'=N_{1}B'$.

3) Выберем симметричную к $N_{1}$ точку $D$ на $(O_{1},r_{1})$ относительно $O_{1}O_{2}$, выберем на $(O_{2},r_{1})$ симметричную точку $N_{1}'$ к точке $N_{1}$ относительно $EF$ и так же $D'$ на той же окружности к $D$ относительно той же прямой. Тогда $D'B' || NA_{1}$ и $N_{1}B = A'D = AD'$ учитывая параллельность получим $AB' = YD'$(равнобедренная трапеция) значит $AD'=B'N_{2}$ как диагонали, тогда $N_{1}B=B'N_{2}$.

4) Опустим высоту $B'N$ тогда $\angle B'NA = \angle AA'B' = 90^{\circ}$ то есть $A,A',B,B',N$ лежат на одной окружности $\omega$ с диаметров $AB'$, откуда и следует что центр $\omega$ лежит на $O_{1}O_{2}$.

А что если уголBMM2=угол180-BNN2

Решение (векторами): Пусть $O$ $-$ центр отрезка $O_1O_2.$ Рассмотрим любую прямую, которая проходит через точку $A.$ Пусть она пересекает $k_1,k_2$ в точках $C_1,C_2$ соответственно. Пусть $C$ $-$ середина отрезка $C_1C_2,$ тогда

$$2\overrightarrow{OC}=\overrightarrow{O_1C_1}+\overrightarrow{O_2C_2}$$

$$\implies 4OC^2=R_1^2+R_2^2+2\overrightarrow{O_1C_1}\cdot\overrightarrow{O_2C_2},$$

где $R_1,R_2$ радиусы $k_1,k_2.$ С другой стороны $\overrightarrow{O_1C_1}\cdot\overrightarrow{O_2C_2}=R_1R_2\cos\angle(O_1C_1,O_2C_2).$

Заметим, что

$$\angle(O_1C_1,O_2C_2)=\angle(O_1C_1,C_1C_2)+\angle(C_1C_2,O_2C_2)=$$

$$\angle(C_1A,O_1A)+\angle(O_2A,C_2A)=\angle(O_2A,O_1A),$$

следовательно $\angle(O_1C_1,O_2C_2)$ не зависит от $C_1C_2.$ Значит длина отрезка $OC$ не зависит от выбора $C_1C_2,$ откуда следует требуемое.