Олимпиада имени Леонарда Эйлера2010-2011 учебный год, II тур регионального этапа

В треугольнике $ABC$ точки $M$ и $N$ — середины сторон $AC$ и $AB$ соответственно. На медиане $BM$ выбрана точка $P$, не лежащая на $CN$. Оказалось, что $PC = 2PN$. Докажите, что $AP = BC$. ( С. Берлов )

Комментарий/решение

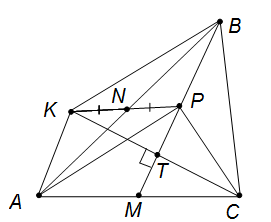
Комментарии от администратора Комментарии от администратора №1.     Решение 1. Отметим точку $K$ такую, что $AKBP$ — параллелограмм. Тогда его диагонали делятся точкой пересечения пополам, то есть пересекаются в точке $N$ и $PK = 2PN = PC$. Пусть прямые $MB$ и $CK$ пересекаются в точке $T$. Поскольку $MT \parallel AK$ и $M$ — середина $AC$, то $MT$ — средняя линия треугольника $AKC$, откуда $KT = TC$. Значит, $PT$ — медиана, проведённая к основанию равнобедренного треугольника $KPC$, откуда $PT \perp CK$. Тогда $BT$ — медиана и высота треугольника $BKC$, значит, $BC = BK$. Наконец, $BK = AP$ так как $AKBP$ — параллелограмм, откуда $AP = BK = BC$.

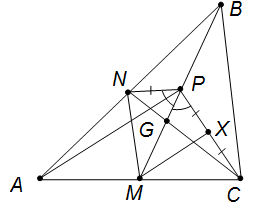
Комментарии от администратора Комментарии от администратора №2.     Решение 2. Обозначим через $G$ точку пересечения медиан треугольника $ABC$. Тогда $CG/GN = 2 = CP/PN$, то есть точка $G$ делит сторону $NC$ треугольника $PNC$ в отношении, равном отношению прилежащих боковых сторон. По признаку биссектрисы получаем $\angle CPG = \angle GPN$. Следовательно, $\angle BPN = \angle BPC$. Пусть $X$ — середина $PC$. Тогда $PX = PN$, поэтому $\angle NPM = \angle XPM $ по двум сторонам и углу между ними. Отсюда $NM = XM$. Наконец, отрезки $XM$ и $NM$ являются средними линиями в треугольниках $APC$ и $ABC$, значит, $AP = 2XM = 2NM = BC$.

Комментарии от администратора Комментарии от администратора №3.     Решение 3. Рассмотрим такую точку $Q$, что $P$ — середина $AQ$. Тогда $BP\parallel QC$, $BQ = 2NP = PC$, т.е. $BQCP$ — равнобочная трапеция $(BQ \parallel NP \Rightarrow$ не параллельна $PC$). Ее диагонали $BC$ и $PQ$ равны, а $PQ = AP$.