Азиатско-Тихоокеанская математическая олимпиада, 2008 год

Рассмотрим функцию $f : \mathbb{N}_0 \to \mathbb{N}_0$, где $\mathbb{N}_0$ — множество неотрицательных целых чисел, которая определяет следующие условия:
(i) $f(0) = 0$,
(ii) $f(2n) = 2f(n)$ и
(iii) $f(2n + 1) = n + 2f(n)$, для всех $n \geq 0$.
(a) Определите три множества $L$, $E$, $G$ такие, что $L= \{n| f(n) < f(n + 1)\}$, $E= \{n | f(n) = f(n + 1)\}$ и $G= \{ n|f(n) > f(n + 1)\}$.
(b) Для каждого $k \geq 0$, найдите общую формулу для $a_k$ относительно $k$, для которой $a_k = \max \{f(n): 0 \leq n \leq 2^k\}$.

Комментарий/решение

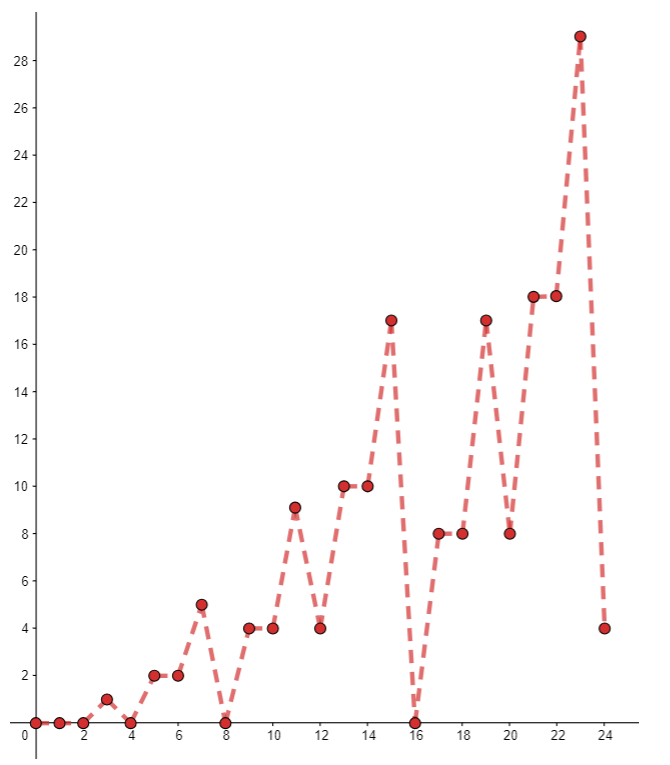
Айталық $Г(f)$ нүктелер жиыны $y=f(n)$ функциясының графигі болсын. Яғни: $Г(f)=\left\{ \left(n,f(n)\right)\in \mathbb{N}_0\times \mathbb{N}_0 | n\in \mathbb{N}_0 \right\}$ $$Г(f)=\left\{0\right\}\cup Г_1 \cup Г_2 \cup ... \cup Г_k \cup... $$

Мұндағы: $ Г_{2k+1}=\left\{ (8k+1,8k),(8k+2,8k),(8k+3,16k+1),(8k+4,8k),(8k+5,16k+2),(8k+6,16k+2),(8k+7,24k+5),(8(k+1)\right\}$

$\qquad \qquad Г_{2k}=\left\{ (16k-7,16k-12),(16k-6,16k-12),(16k-5,24k-15),(16k-4,16k-12),(16k-3,24k-14),(16k-2,24k-14),(16k-1,32k-15),(16k)\right\}$

$$\color{red}{\textbf{a)}} L=\left\{2k| k\in \mathbb{N} \right\}, \qquad \mathbb{N}=\mathbb{N}_0 \diagdown \left\{0\right\} $$

$$ E=\left\{4k+1| k\in \mathbb{N}_0 \right\} \cup \left\{0\right\} $$

$$ G=\left\{4k+3 | k\in \mathbb{N}_0\right\}$$

$$\color{red}{\textbf{b)}} a_k=\max\left\{f(n)|0\leq n \leq 2^k\right\}$$

$$ Г_1:$$

$$ a_0=\max\left\{f(k)| 0\leq k \leq 1\right\}=0$$

$$ a_1=\max\left\{f(k)| 0\leq k \leq 2\right\}=0=f(1)=f(2^1-1)$$

$$ a_2=\max\left\{f(k)| 0\leq k \leq 4\right\}=1=f(3)=f(2^2-1)$$

$$ a_3=\max\left\{f(k)| 0\leq k \leq 8\right\}=5= f(7)=f(2^3-1)$$

$$ Г_2:$$

$$ a_4=\max\left\{f(k)| 0\leq k \leq 16\right\}=17=f(15)=f(2^4-1)$$

$$ Г_3:$$

$$ a_5=\max\left\{f(k)| 0\leq k \leq 32\right\}=49=f(31)=f(2^5-1)$$

$$\Rightarrow a_k=f(2^k-1)=f(2(2^{k-1}-1)+1)=2^{k-1}-1+2f(2^{k-1}-1)=$$

$$=2^{k-1}-1+2(2^{k-2}-1+2f(2^{k-2}-1))=2\cdot 2^{k-1}-1-2+4f(2^{k-2}-1))=...=$$

$$=k\cdot 2^{k-1} -(1+2+2^2+...+2^{k-1})=k\cdot 2^{k-1} -(2^k-1) \Rightarrow$$

$$ a_k=k\cdot 2^{k-1} -(2^k-1)=2^{k-1}(k-2)+1$$

$$\color{red}{\textbf{Жауабы:}} \textbf{a)} L=\left\{2k| k\in \mathbb{N} \right\}, \quad E=\left\{4k+1| k\in \mathbb{N}_0 \right\} \cup \left\{0\right\} \quad G=\left\{4k+3 | k\in \mathbb{N}_0\right\}$$

$$\textbf{b)}a_k=2^{k-1}(k-2)+1$$