6-я Международная Жаутыковская олимпиада, 2010 год

Все стороны треугольника $ABC$ различны. Пусть $O$, $I$, $H$ — соответственно центр описанной окружности, центр вписанной окружности и точка пересечения высот треугольника $ABC$. Докажите, что
a) $\angle OIH > 90^\circ$;
b) $\angle OIH > 135^\circ$.

Комментарий/решение

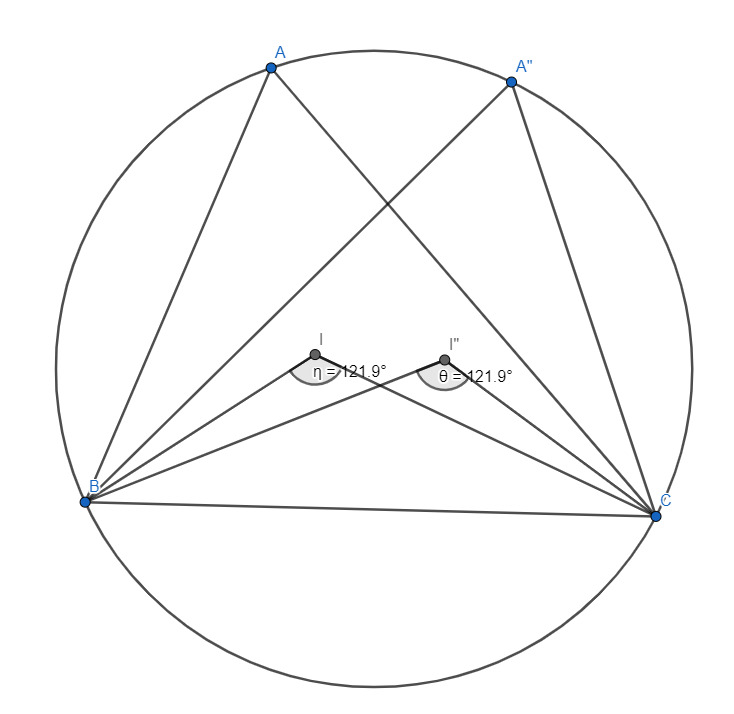
Лемма 1 : если мы построим второй треугольник с точкой $A'$,которая лежит на описанной окружности ,то значение $\angle BIC=\angle BI'C$, где $I'$ центр вписанной окружности$\triangle A'BC$ (имеется ввиду что $\angle BIC=const$ при выборе точки $A'$ на описанной окружности) и дополнительное условие то что $A'$ лежит на $\overset\frown{BC}$ которая содержит $A$

Доказательство: так как $\angle ABC$ и $\angle A'BC$ смотрят на одну дугу $\angle BAC=\angle BA'C$, дальше простой счет углов.

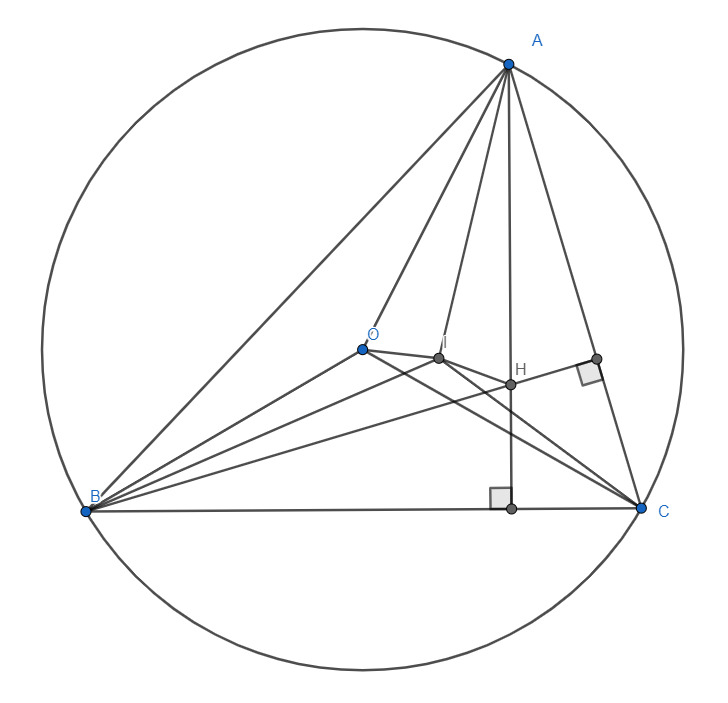
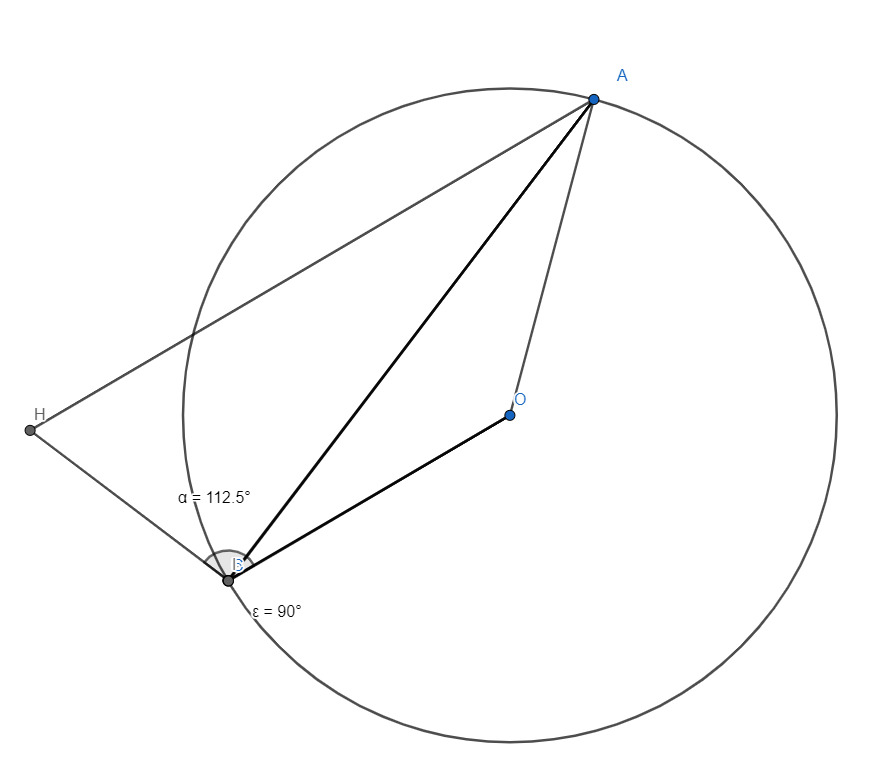
а) Так как нам нужно доказать что $\angle OIH>90^\circ$ нам достаточно показать что $\angle BIC\geq90^\circ$, так как по нашей лемме $\angle BIC=const$ при любом A на описанной окружности, $\angle BIC$ зависит от точек $B,C$ рассмотрим крайний случай, когда $B$ и $C$ совпадают, так как при этом раскладе $\angle BIC$ минимальный, тогда $BC$ совпадет с высотой откуда $\angle ABH=\angle BIC=90^\circ$, получается что минимальное значение $\angle BIC=90^\circ$, что доказывает первый пункт.

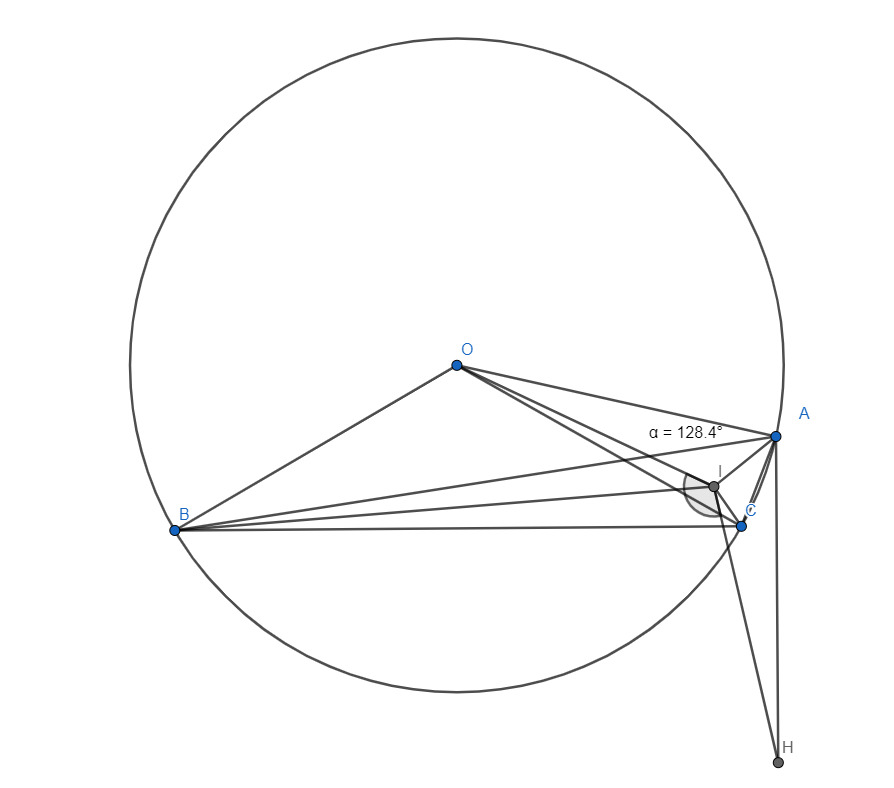
б) Кажется в этом пункте должно быть какое то дополнительное условие, так как найдется такое расположение A на окружности, что $\angle BIC<135^\circ$, пример на рисунке.

Треугольник остроугольный