5-я Международная Жаутыковская олимпиада, 2009 год
Комментарий/решение:
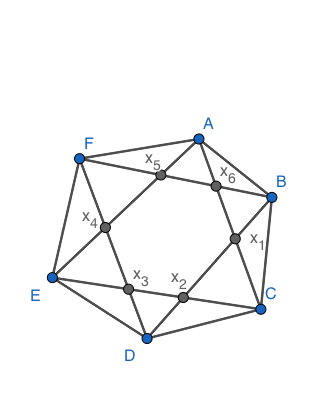
Пусть $x_{1},x_{2}...,x_{6}$ углы как показаны на рисунке.
Преобразовав неравенство
$$BD \cdot AC + BF \cdot AC + DF \cdot CE + DB \cdot CE \\ + DF \cdot AE + BF \cdot AE \geq 2 \sqrt{3}S \\+ DF \cdot AC + BF \cdot CE + BD \cdot AE$$
Выразив площадь шестиугольника
$S=S_{ABCD}+S_{AFED}= \frac{BD \cdot AC \cdot \sin(x_{1})}{2} \\ + \frac{DF \cdot AE \sin(x_{4})}{2}$
Аналогично и $S=S_{ABCF}+S_{FEDC}$ и $S=S_{BCDE}+S_{AFBE}$
Суммирую все три выражения и поделив на $3$ получаем формулу площади $S$ выраженную через вышеописанные углы , тогда подставляя это в неравенство и приводя подобные, получаем
$BD \cdot AC(1-\dfrac{\sin(x_1)}{\sqrt{3}}) + BF \cdot AC(1-\dfrac{\sin(x_6)}{\sqrt{3}}) \\DF \cdot AE(1-\dfrac{\sin(x_4)}{\sqrt{3}}) + BF \cdot AE(1-\dfrac{\sin(x_5)}{\sqrt{3}}) \\DF \cdot CE(1-\dfrac{\sin(x_3)}{\sqrt{3}})+BD \cdot CE(1-\dfrac{\sin(x_2)}{\sqrt{3}}) \\ \geq DF \cdot AC + BF \cdot CE + BD \cdot AE$
Из треугольника $BDF$
$BD+BF=DF \left( \frac{\sin(x_4+x_5)+\sin(x_2+x_3)}{\sin(x_1+x_6)} \right) $
$DF+BF=BD \left( \frac{\sin(x_2+x_3)+\sin(x_1+x_6)}{\sin(x_4+x_5)} \right) $
$BD+DF=BF \left( \frac{\sin(x_1+x_6)+\sin(x_4+x_5)}{\sin(x_2+x_3)} \right) $
Тогда снова приводя подобные учитывая то что выше, для удобства заменив выражения отличных от сторон, получаем
$AC \cdot DF(n-1) + BD \cdot AE(m-1) + \\ BF \cdot CE(t-1) \geq 0$
Заключительный раз выражая $BD,BF$ через $DF$ и $AE,CE$ через $AC$ преобразуя и сокращая на положительное $AC \cdot DF$ окончательно получаем неравенство
$\frac{\sin(x_4+x_5)(\sin(x_3+x_4) \sin(x_1) + \sin(x_5+x_6)\sin(x_2))}{ \sin(x_4+x_5)(\sin(x_3+x_4) + \sin(x_5+x_6) - \sin(x_1+x_2)) + \sin(x_1+x_6)}$
$\frac{ + \sin(x_1+x_6)(\sin(x_5+x_6) \cdot \sin(x_3) + \sin(x_1+x_2) \cdot \sin(x_4))}{(\sin(x_5+x_6)+ \sin(x_1+x_2) - \sin(x_3+x_4))+\sin(x_2+x_3)}$
$\frac{+\sin(x_2+x_3)(\sin(x_1+x_2) \cdot \sin(x_5) + \sin(x_3+x_4) \cdot \sin(x_6))}{(\sin(x_1+x_2)+ \sin(x_3+x_4) - \sin(x_5+x_6))}$
$\leq \sqrt{3}$
При условий что $x_1+x_2+x_3+x_4+x_5+x_6=720^{\circ}$
Отметим что равенство достигается когда $x_1=x_2=x_3=x_4=x_5=x_6=120^{\circ}$
Покажем что только при этих значениях выражение выше достигает своего максимума.
1)
Пусть $(x_{1},x_{2},x_{3},x_{4},x_{5},x_{6})=(a,a,a,a,a,b)$ (Порядок не важен, так как функция на выходе одна и та же) откуда $b=720-5a$
Подставляя в выражение $N$, получаем
$$N(a)=\dfrac{-3sina \cdot (2\cos2a-1)}{4\cos^2(2a)+2}$$
Найдя $N’(a)= \dfrac{\sqrt{27} \cdot \cos(\frac{\pi}{6}-a)}{ (2\sin(\frac{\pi}{6}-a)-1)^2}=0$
Откуда $a = \dfrac{2\pi}{3}=120^{\circ}$ проверяя получаем, что функция в данной точке достигает максимума равной $\sqrt{3}$.
2) Пусть $(x_{1},x_{2},x_{3},x_{4},x_{5},x_{6})=(a,a,a,a,b,c)$ выражая $c=720-4a-b$ подставив получаем
$$N=\frac{-3sina \cdot cos(2a+b)}{2\cos2a(\cos(2a+b)+cosa)+2 cosa}$$
Рассмотрим как функцию при фиксированном значений $a$ тогда
$N’=\dfrac{3 \sin2a(\cos2a+1) \cdot \sin(2a+b)}{(2\cos2a(\cos(2a+b)+cosa)+2 \cdot cosa)^2}$
$=0$ откуда $sin(2a+b)=0$ откуда $b=360-2a$
Значит рассмотрев числа $(x_{1},x_{2},x_{3},x_{4},x_{5},x_{6})=(a,a,a,a,360-2a$ $,360-2a)$ аналогичными рассуждениями $(1)$ получаем так же $N_{max}=\sqrt{3}$ при $a=120^{\circ}$
3)
Значит каким бы ни были углы $x_{1}...x_{6}$ рассуждениями как в пункте $(2)$ выражения будет постепенно сводится к $(1)$ и при шести различных, пяти итд переменных, откуда и следует утверждение.

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.