11-я Международная Жаутыковская олимпиада, 2015 год

Точка $M$ лежит внутри треугольника $ABC$. Прямая $BM$ пересекает сторону $AC$ в точке $N$. Точка $K$ симметрична $M$ относительно $AC$. Прямая $BK$ пересекает $AC$ в точке $P$. Докажите, что если $\angle AMP=\angle CMN$, то $\angle ABP=\angle CBN$. ( Н. Седракян )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Первое решение. Пусть $D$, $E$ и $F$ — основания перпендикуляров, опущенных из $A$ на $BP$, $MP$ и $BM$ соответственно, а $G$, $Q$ и $H$ — основания перпендикуляров, опущенных из $C$ на $BP$, $MP$ и $BM$ соответственно. Заметим, что $\triangle AFM\sim \triangle CQM$ и $\triangle AME\sim \triangle CMH$, следовательно, ${AF\over CQ}={AM\over CM}= {AE\over CH}$. В силу симметрии $CQ=CG$, $AE=AD$ и $\angle FAD=\angle FBD=\angle GCH$, поэтому ${AF\over CG}={AD\over CH}$. Отсюда следует, что $\triangle FAD\sim \triangle GCH$, таким образом, $\angle AFD=\angle CGH$. Далее, точки $A$, $B$, $F$, $D$ лежат на одной окружности, поэтому $\angle ABP=\angle AFD$, и аналогично $\angle CBN=\angle CGH$. Сопоставляя это равенство с результатом предыдущего абзаца, получаем $\angle ABP=\angle CBN$.

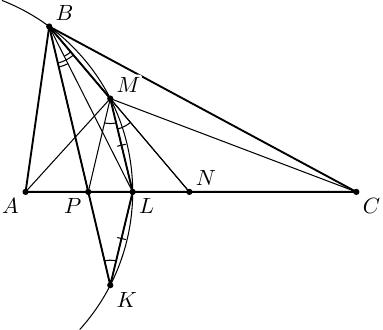
Комментарии от администратора Комментарии от администратора №2.     Второе решение. Пусть $L$ — основание биссектрисы из вершины $M$ в треугольнике $PMN$. Тогда из условия задачи следует, что $\angle AML=\angle LMC$. Следовательно, точки $M,L,K$ лежат на окружности Аполлония $\omega $ для точек $A$ и $C$. Из симметрии заметим, что $\angle NML=\angle LMP=LKP$. Тогда $\angle BKL+\angle BML=\angle BLK+180{}^\circ -\angle NML=180{}^\circ $, то есть четырёхугольник $BMLK$ вписанный. Значит, точка $B$ также лежит на $\omega $, откуда $\angle ABL=\angle LBC$ и $\angle KBL=\angle LBM$, в силу того, что $KL=LM$. Откуда и следует утверждение задачи.

Заметим что $\angle AKP=\angle CKN$ и что $A$ и $C$ лежат биссектрисе $\angle BNK$. Значит $A$ и $C$ Изогонально сопрежены относительно $\triangle BNK$ следовательно $\angle ABP=\angle CBN$ :)