Олимпиада имени Леонарда Эйлера2014-2015 учебный год, I тур регионального этапа

Серединные перпендикуляры к сторонам $AB$ и $BC$ выпуклого четырёхугольника $ABCD$ пересекают стороны $CD$ и $DA$ в точках $P$ и $Q$ соответственно. Оказалось, что $\angle APB = \angle BQC$. Внутри четырёхугольника выбрана точка $X$ такая, что $QX \parallel AB$ и $PX \parallel BC$. Докажите, что прямая $BX$ делит диагональ $AC$ пополам. ( С. Берлов )

Комментарий/решение

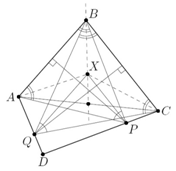
Комментарии от администратора Комментарии от администратора №1.     Решение. Достаточно доказать, что расстояния от точек $A$ и $C$ до прямой $BX$ равны. Это равносильно тому, что $S_{ABX} = S_{BCX}$, поскольку у треугольников $ABX$ и $BCX$ общее основание $BX$. Поскольку $QX \parallel AB$, имеем $S_{ABX} = S_{ABQ}$. Аналогично, $S_{CBX} = S_{CBP}$. Заметим, что равнобедренные треугольники $ABP$ и $CBQ$ подобны по двум углам, поэтому $AB/BC = BP/BQ$, откуда $AB \cdot BQ = CB \cdot BP$. Так как $\angle ABP = \angle CBQ$, то и $\angle ABQ = \angle CBP$. Следовательно, площади треугольников $ABQ$ и $CBP$ относятся как произведения заключающих равные углы сторон, т. е. эти площади равны. Но тогда $S_{ABX} = S_{ABQ} = S_{CBP} = S_{CBX}$, что и требовалось доказать.