XIV математическая олимпиада «Шелковый путь», 2015 год

Пусть $O$ — центр окружности, описанной около остроугольного треугольника $ABC$. Рассмотрим две окружности $\omega$ и $\Omega$, вписанные в угол $BAC$ таким образом, что $\omega$ касается внешним образом дуги $BOC$ окружности, описанной около треугольника $BOC$; а окружность $\Omega$ касается внутренним образом окружности, описанной около треугольника $ABC$. Докажите, что радиус $\Omega$ вдвое больше радиуса $\omega$. ( Ильясов С. )

Комментарий/решение

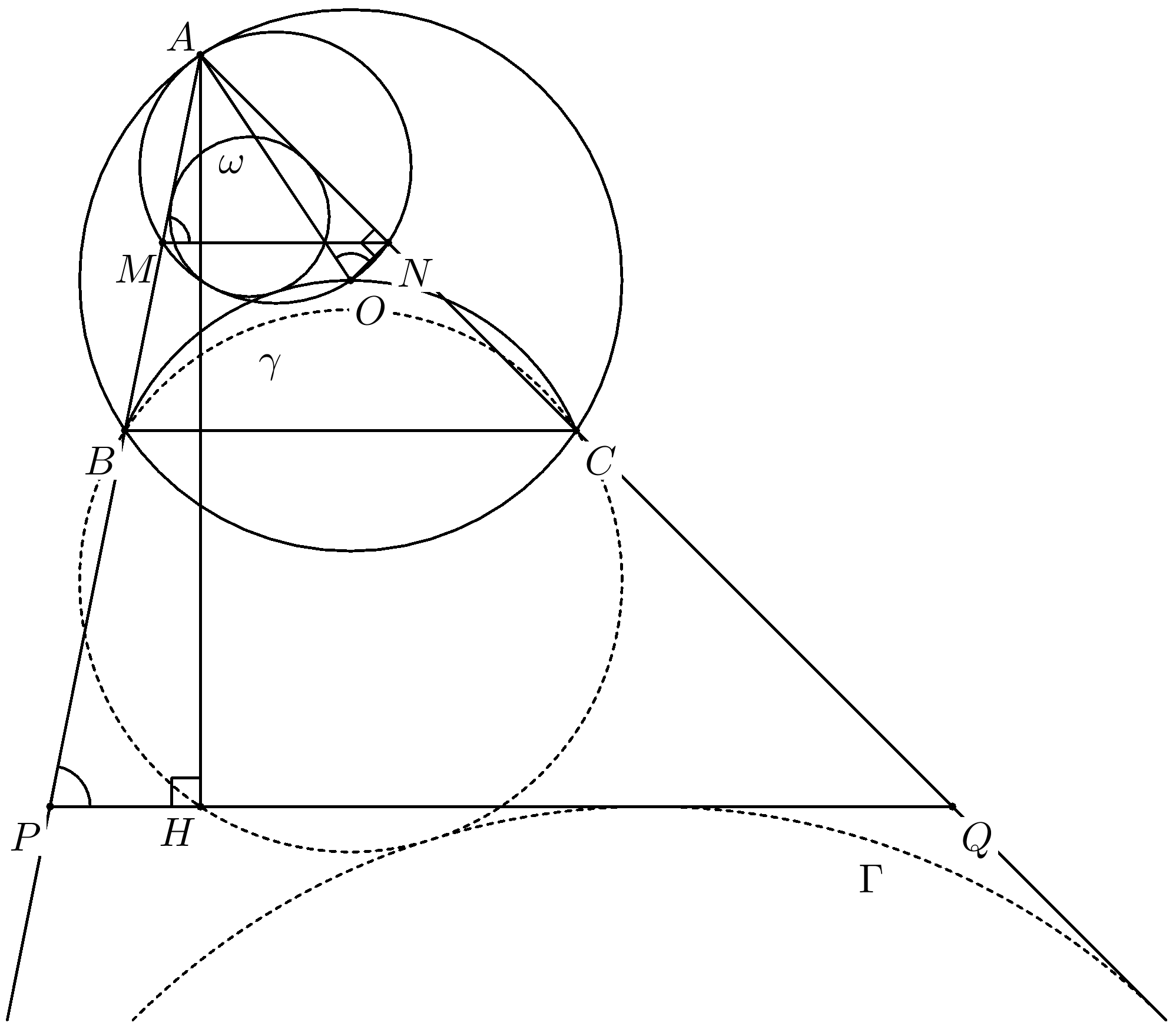
Комментарии от администратора Комментарии от администратора №1.     Отметим точки $P$ и $Q$ симметричные вершине $A$ относительно $B$ и $C$ соответственно. Пусть $M$ и $N$ — середины сторон $AB$ и $AC$ соответственно. В треугольнике $APQ$ проведем высоту $AH$. Заметим, что точки $A$, $M$, $N$ и $O$ лежат на окружности с диаметром $AO$. Поэтому $\angle AON = \angle AMN =\angle APQ$. Так как треугольники $AON$ и $APH$ — прямоугольные и $\angle AON = \angle APQ$, то они подобны. Значит $AO \cdot AH = AN \cdot AP = \frac{AC}{2}\cdot 2AB=AC \cdot AB$.
Рассмотрим композицию инверсии с центром в точке $A$ радиусом $r =\sqrt{AB \cdot AC}$ и симметрии относительно биссектрисы угла $BAC$. Такая композиция меняет местами точки $O$ и $H$, а также точки $B$ и $C$. Значит, окружность, проходящая через точки $B$, $O$ и $C$, перейдет в окружность $\gamma$, проходящую через точки $B$, $H$ и $C$ (т. е. в окружность девяти точек треугольника $APQ$). Образом окружности $\omega$ при такой композиции перейдет в окружность, вписанную в угол $BAC$ и касающуюся (внешним образом) дуги $BHC$ окружности $\gamma$ (очевидно, что такая окружность единственная).
С другой стороны, в силу теоремы Фейербаха, вневписанная окружность $\Gamma$ треугольника $APQ$ (соответствующая вершине $A$) касается (внешним образом) дуги $BHC$ окружности $\gamma$. Значит $\Gamma$ — образ окружности $\omega$. Стало быть $\omega$ касается образа прямой $PQ$, т. е. описанной окружности треугольника $AMN$ (т. к. ${AM \cdot AB }= {AB \cdot AC} ={ AN \cdot AP}$). Таким образом, гомотетия с центром в $A$, переводящая треугольник $AMN$ в $ABC$, переводит $\omega$ в $\Omega$. Последнее завершает доказательство.