Городская Жаутыковская олимпиада, 7 класс, 2003 год

В равнобедренном треугольнике $ABC$ ($AB=AC$, $\angle BAC=30{}^\circ $) на стороне $AB$ и медиане $AD$ соответственно выбраны точки $Q$ и $P$ таким образом, что $PC=PQ$ ($P\ne Q$). Найдите $\angle PQC$.

Комментарий/решение

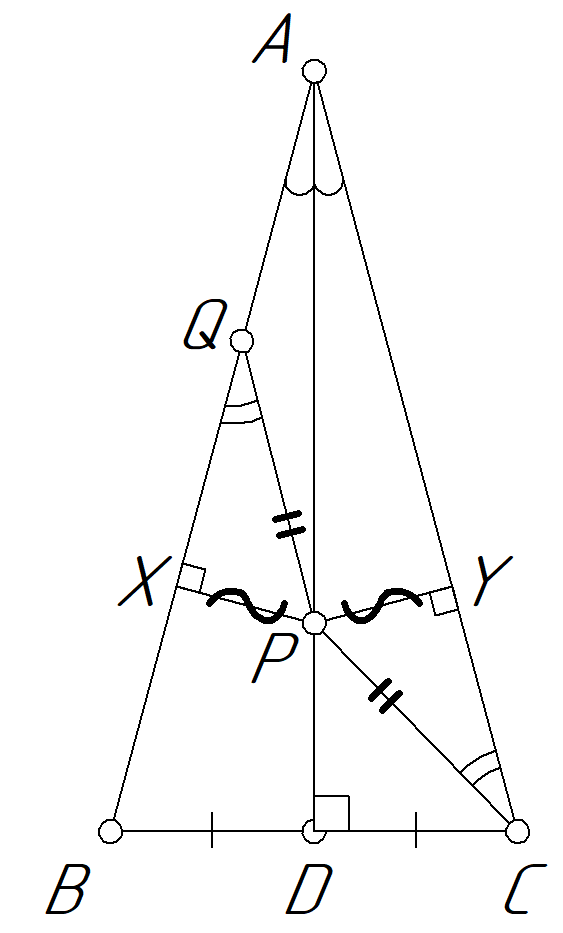
Ответ: $15^{\circ}$

Решение.

1) Теорема: в равнобедренном треугольнике медиана, проведённая к основанию, также является и высотой, и биссектрисой.

На основании теоремы $(1)$ имеем $\angle BAD=\angle CAD;\angle ADC=90^{\circ}$

2) Восстановим перпендикуляры из точки $P$. Получаем по построению $\angle PXQ=\angle PYC$

3)$\triangle AXP=\triangle AYP$. Это следует из теоремы $(2)$

Теорема $(2)$: если у треугольников равны сторона и два соответствующих угла, то они равны. Действительно, сторона $PA-$ общая, $\angle PXQ=\angle PYC;\angle BAD=\angle CAD$

Из пункта $(3)$ важный вывод: $PX=PY$

4)Покажем, что $\triangle PXQ=\triangle PYC$

$PX=PY;PQ=PC$

Признак равенства треугольников: по равным гипотенузе и катету

Из пункта $(4)$ важный вывод: $\angle PQX=\angle PCY$

5) Рассмотрим четырехугольник $CPQA$. Сумма его углов $360^{\circ}$

$\angle ACP+\angle CPQ+\angle PQA+\angle QAC=360^{\circ}$

$\angle CPQ=360^{\circ}-(\angle ACP+\angle PQA)-\angle QAC)$

В сумме $\angle ACP$ и $\angle PQA$ дадут $180^{\circ}$. Отсюда

$\angle CPQ=360^{\circ}-180^{\circ}-30^{\circ}=150^{\circ}$

6) Рассмотрим $\triangle PQC$. Он равнобедренный, поэтому $\angle PQC=\dfrac{180^{\circ}-150^{\circ}}{2}=15^{\circ}$