Городская Жаутыковская олимпиада, 8 класс, 2004 год

В прямоугольном треугольнике $ABC$ на катетах $AB$ и $BC$ ($2BC > AB > BC$) взяты точки $D$ и $E$ так, что$AD=CB$, $BD=CE$. Докажите, что угол между отрезками $AE$ и $CD$ равен $45{}^\circ $.

Комментарий/решение

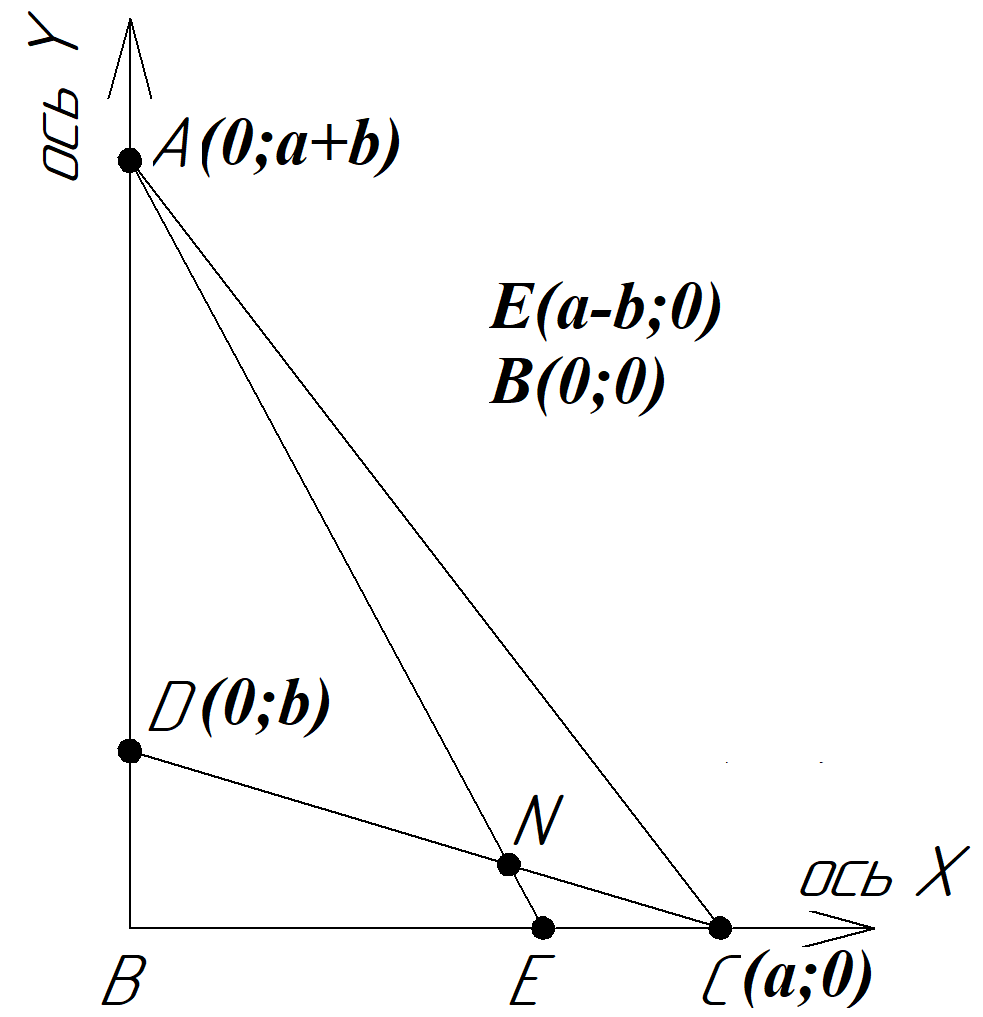
Рассмотрим вектора $\overrightarrow{CD}$ и $\overrightarrow{EA}$. Косинус между этими векторами равен $$\ cos(\overrightarrow{CD};\overrightarrow{EA})= \cos \angle DNA=\dfrac{\overrightarrow{CD}\cdot \overrightarrow{EA}}{|\overrightarrow{CD}|\cdot |\overrightarrow{EA}|}$$ Вектор $\overrightarrow{CD}=(-a;b);$ вектор $\overrightarrow{EA}=(-a+b;a+b);$

Скалярное произведение векторов: $\overrightarrow{CD}\cdot \overrightarrow{EA}=(-a)\cdot {(-a+b)}+b\cdot {(a+b)}=a^2+b^2$

Длины векторов: $|\overrightarrow{CD}|=\sqrt{(-a)^2+b^2}=\sqrt{a^2+b^2}$

$|\overrightarrow{EA}|=\sqrt{(-a+b)^2+(a+b)^2}=\sqrt{2\cdot {(a^2+b^2)}}$

Отсюда косинус искомого угла равен

$\ cos(\overrightarrow{CD};\overrightarrow{EA})=\dfrac{a^2+b^2}{\sqrt{a^2+b^2}\cdot {\sqrt{2\cdot {(a^2+b^2)}}}}=\dfrac {1}{\sqrt 2}=\dfrac{\sqrt 2}{2}$

$\arccos(\dfrac{\sqrt 2}{2})=\dfrac{\pi}{4}$

Что и требовалось доказать

PS. Вполне возможно,есть способ, доступный восьмикласснику. Просто выкладываю первое, что пришло в голову. Вектора таки упрощают эту задачу почти до уровня учебной

N-точка пересечения $AE \cap CD$

$E'$ точка симметричная относительно $С$ к точке $E$, $F$ - середина $AE$ и $G$ середина $AB$ тогда $GD=GF$ так как $GF=\dfrac{BE}{2} = \dfrac{AD-BD}{2} , \ GD=\dfrac{AB}{2}-BD = \dfrac{AD+BD}{2}-BD = GF$ и $\angle DFC = 90^{\circ}$ нужно показать что из теоремы Пифагора $\dfrac{(AD-BD)^2}{2}+CF^2 = BD^2+AD^2$ что верно , так как $CF^2=\dfrac{AE^2}{4} = \dfrac{AB^2}{2} = \dfrac{(AD+BD)^2}{2}$

Значит $BDFC$ вписанный, если $FN$ пересекает эту окружность в точке $H$ тогда $CE=CH$ так как $FB=FE$ откуда $\angle DCB =\angle DFB = \angle CFH = \angle E'AE$ опираются на равные хорды, откуда $ANCE'$ вписанный , откуда $\angle CNE = 45^{\circ}$.