Городская Жаутыковская олимпиада, 8 класс, 2011 год

В прямоугольник вписан четырехугольник (по вершине на каждой стороне). Докажите, что его периметр не меньше удвоенной диагонали прямоугольника.

Комментарий/решение

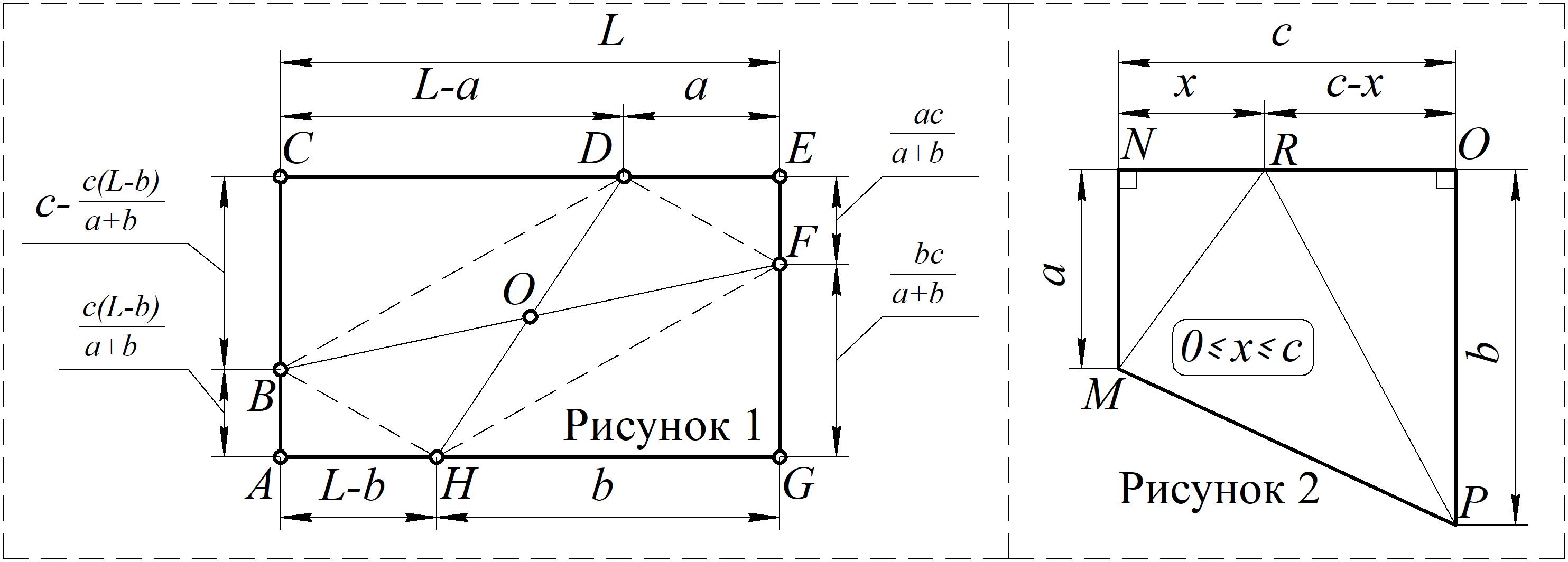
1)Рассмотрим небольшую предзадачу.Рассмотрим прямоугольную трапецию $MNOP$ (см.рис.2). Интересно для данной

фигуры найти положение точки $R$, дающее наименьший периметр треугольнику $MRP$.Так как точки $M$ и $P$

фиксированы, задача сводится к $(MR+PR)\rightarrow \min$

2)По теореме Пифагора

$$f(a,b,c,x)=MR+PR=\sqrt{a^2+x^2}+\sqrt{b^2+(c-x)^2}$$

3)Ищем стационарные точки функции $f(a,b,c,x)$

$$\dfrac{\partial f}{\partial x} = \dfrac{x}{\sqrt{a^2+x^2}} - \dfrac{c-x}{\sqrt{b^2+(c-x)^2}}=0$$

Корни данного уравнения $x_1 = \dfrac{ac}{a+b}$ и $x_2 = \dfrac{ac}{a-b}\ge \dfrac{(a-b)c}{a-b}=c$

По смыслу подходит только $x_1$. Остается проверить, правда ли полученная стационарная точка минимум

(взять вторую производную, и по ее знаку понять, min или max).По итогу проверки, получилось min.

4)Обозначим $DE = a;HG=b;CE=L$.Вместо того, чтобы сделать сразу условие $P_{BDFH}\rightarrow \min$,

потребуем отдельно минимума периметра треугольников $\Delta DFH,\Delta BFH,\Delta BDF,\Delta BDH$.

5)Тогда, для достижения минимального периметра $\Delta DFH$, расположим точку $F$ так,

что $EF = \dfrac{ac}{a+b};FG = \dfrac{bc}{a+b}$ (пункт 3)

6)Обозначим $AB = x;AH = L-b$. Чтобы периметр $\Delta BFH$ оказался минимальным, также применим (3) к трапеции $ABFG$

$$HG = \dfrac{\dfrac{bc}{a+b}\cdot L}{\dfrac{bc}{a+b}+x}=b\;\rightarrow x=\dfrac{c}{a+b}\cdot (L-b)=AB$$

Отсюда $BC=AC-AB=c-\dfrac{c}{a+b}\cdot (L-b)=\dfrac{c}{a+b}\cdot (a+2b-L)$

7)Чтобы периметр $\Delta BDF$ оказался минимальным, также применим (3) к трапеции $BCEF$

$$DE=\dfrac{EF\cdot L}{CB+EF}=a\Rightarrow a=\dfrac{\dfrac{ac}{a+b}\cdot L}{\dfrac{c}{a+b}\cdot (2a+2b-L)}$$

Данное уравнение сводится к $L=a+b$.

8)При условии $L=a+b$ четырехугольник $BDFG$ - параллелограм. Доказательство: $\Delta BAH = \Delta FED$ по двум катетам, значит, $BH=DF$.

И правда,$$AB=\dfrac{(L-b)c}{a+b}=\dfrac{ac}{a+b}=EF$$

Аналогично $\Delta BCD = \Delta FGH$ по двум катетам, значит, $BD=HF$.

Из попарного равенства противоположных сторон $BDFG$ следует, что $BDFG$- параллелограм.

9)Посчитаем периметр $BDFG$ при условии $L=a+b$

$$P_{BDFH}=2\cdot (DF+HF) = 2\cdot\left(\sqrt{a^2+\dfrac{a^2c^2}{L^2}}+\sqrt{b^2+\dfrac{b^2c^2}{L^2}} \right)$$

$$P_{BDFH}=2\cdot\left(\dfrac{a}{L}\sqrt{L^2+c^2}+\dfrac{b}{L}\sqrt{L^2+c^2} \right)=2\cdot\dfrac{a+b}{L}\sqrt{L^2+c^2}=2\sqrt{L^2+c^2}$$

Остается заметить, что $\sqrt{L^2+c^2}$ - это длина диагонали.

Вывод: Показано, что наименьший периметр искомого четырехугольника не меньше 2 длин диагоналей. Утверждение задачи доказано полностью.

дядя не нада

Ахахах))Папич

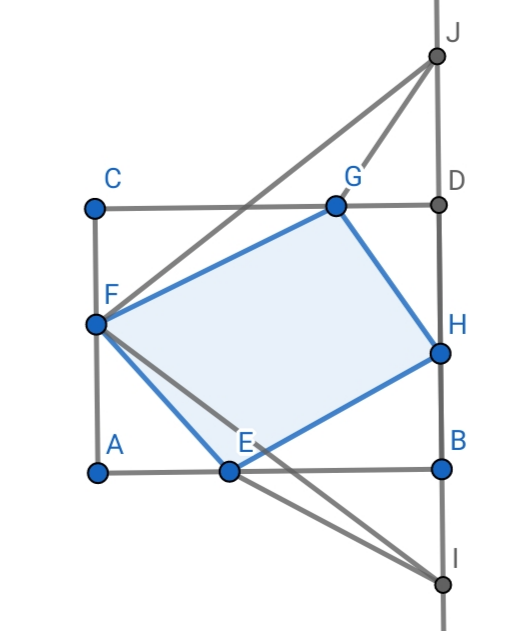
Пусть вершины четырёхугольника $E,F,G,H$ лежат на сторонах $AB,AC,CD,DB$ прямоугольника $ACDB$. Пусть $I,J$ симметричны $H$ относительно $B$ и $C$, соответственно. Тогда $$P_{EFGH}=EF+FG+GH+HE=(FE+EI)+(FG+GH)\ge FI+FJ$$по неравенству ломаной для $FEI$ и $FGJ$. Также имеем $IJ=2BD$

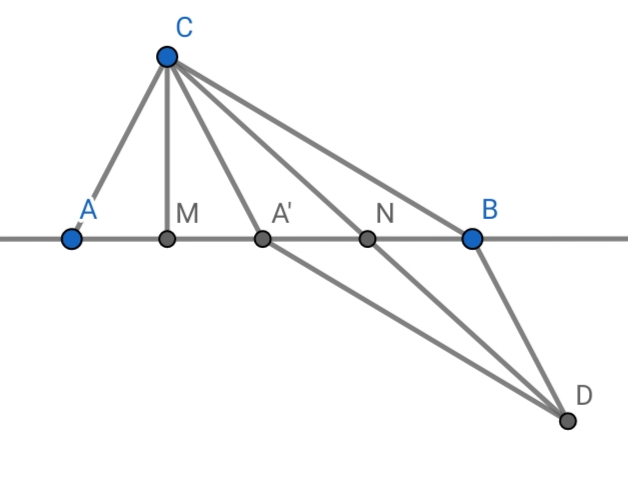
Для фиксированного $F$ докажем, что $FI+FJ$ достигает минимума, когда $H$ - основание перпендикуляра из $F$ и при этом $FI=FJ$(на чертеже $C,A,B$ это $F,I,J$, соответственно)

Пусть $M$ - основание перпендикуляра из $C$, $A'$ симметрична $A$ относительно $M$, $N$ - середина $A'B$, $D$ на прямой $CN$ такова, что $CN=ND$. Тогда $A'CBD$ параллелограмм, откуда $$CA+CB=CA'+CB=CA'+A'D\ge CD=2CN$$Заметим, что $2MN=AB$, то есть $N$ фиксированно, что требовалось. Осталось лишь показать, что если $FG+FI$ достиг минимума, то $FI=FG=AD$, что совсем несложно