Республиканская олимпиада по математике, 2014 год, 11 класс
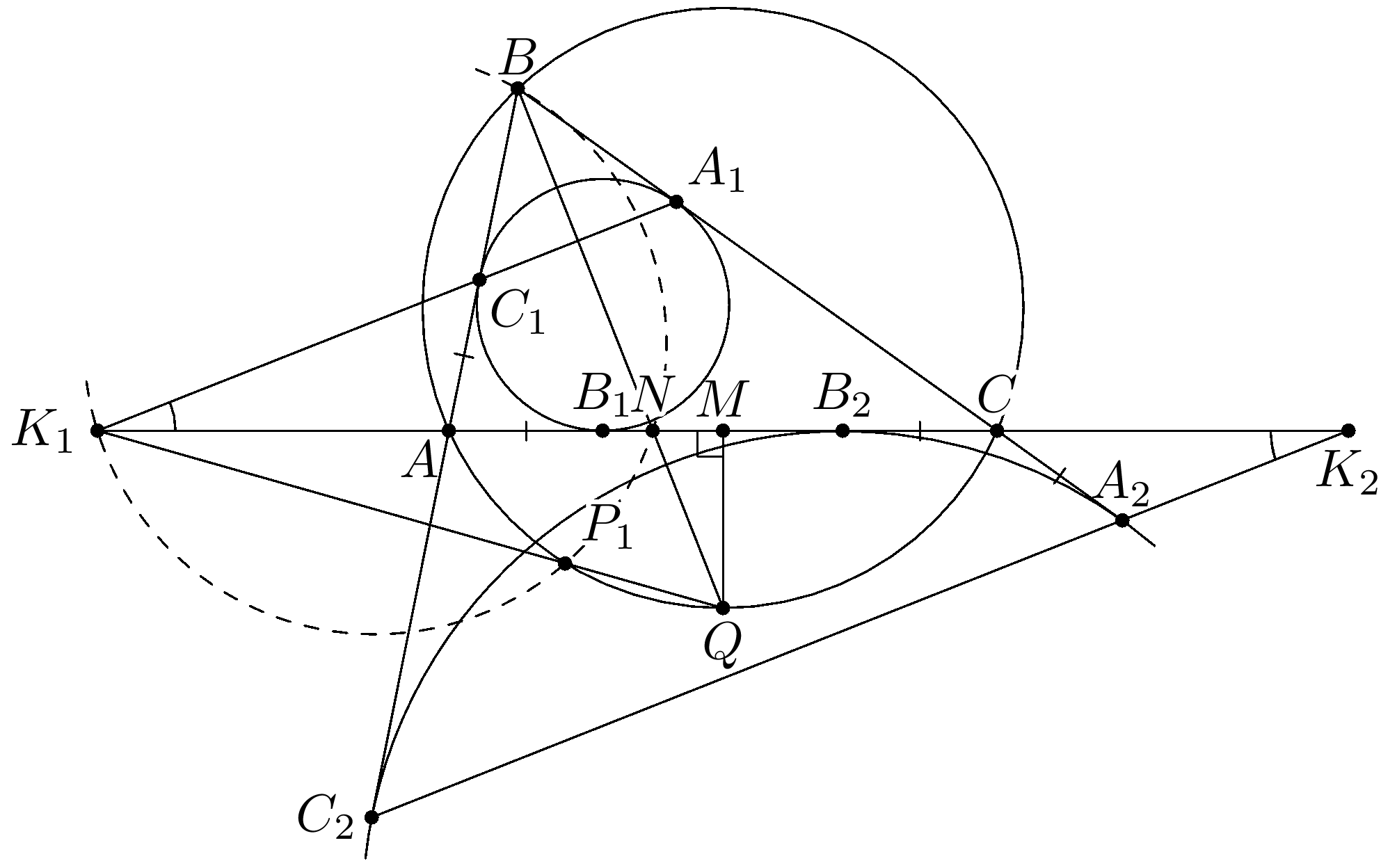
В неравнобедренном треугольнике $ABC$ вписанная окружность
касается сторон $AB$ и $BC$ в точках $C_1$ и $A_1$ соответственно,
а вневписанная окружность (касающаяся стороны $AC$) — соответственно
в точках $C_2$ и $A_2$.
Точка $N$ — основание биссектрисы из вершины $B$.
Прямая $A_1C_1$ пересекают прямую $AC$ в точке $K_1$. Пусть описанная
окружности треугольника $BK_1N$ повторно пересекают описанную окружность треугольника $ABC$ в точке $P_1$.
Аналогично определим точки $K_2$ и $P_2$. Докажите, что $AP_1 = CP_2$.
(
М. Кунгожин
)
посмотреть в олимпиаде
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1. Не теряя общности положим $BC > AB$. Пусть $M$ — середина $AC$, а $BN$ пересекает описанную окружность треугольника $ABC$ в точке $Q$. Пусть вписанная в вневписанная окружности касаются $AC$ в точках $B_1$ и $B_2$ соответственно.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.