33-я Международная Математическая OлимпиадаРоссия, Москва, 1992 год

В пространстве даны 9 точек, никакие четыре из которых не лежат в одной плоскости. Все эти точки попарно соединены отрезками. Отрезок может быть закрашен в синий или красный цвет или остаться незакрашенным. Найти наименьшее значение $n$ такое, что при любом закрашивании любых $n$ отрезков найдется треугольник, все стороны которого будут закрашены в один цвет.

Комментарий/решение

Ответ: $33$

Степенью вершины - называется число ребер графа, которым принадлежит эта вершина, в данном случае $A(n)$ где $A$ вершина и $n$ его степень.

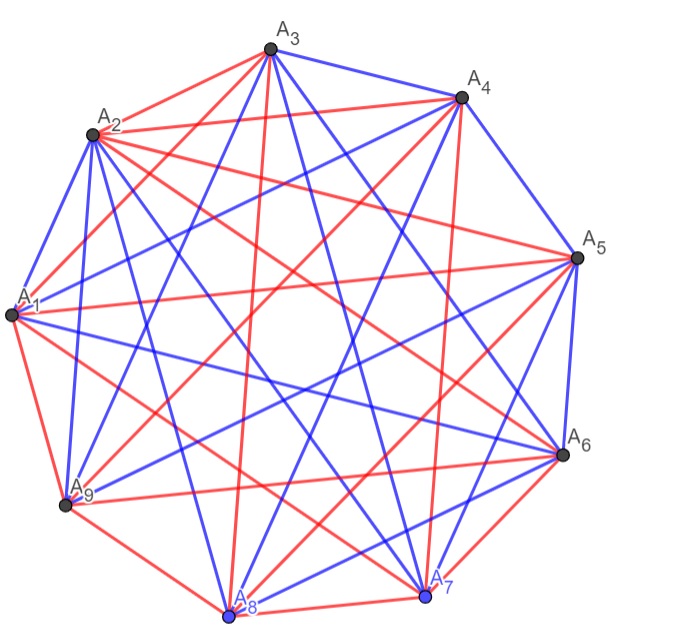
1) Рассмотрим формально граф $G$ с вершинами $A_{1},A_{2},...,A_{9}$ будем идти от обратного, найдем максимальное состояния графа, при котором не найдется треугольник закрашенный в один цвет, пример построения приведен в (рис). То есть $4$ вершины имеют степень $V(7)$ другая половина так же $V(7)$ и одна $V(3)=8$ причем у первой закрашены $4$ красных и $3$ синих, другая обратно и одна поровну. (есть другие вариации, но структура графа та же) и того получаем всего ребер = $\dfrac{7 \cdot 8+8}{2} = 32$.

2) Докажем что количество ребер $33$ быть не может при данных закрашивании. Ребер $33$ тогда сумма вершин $33 \cdot 2 = 66$ так как $66=7 \cdot 9+3$ то есть как минимум $3$ вершины должны иметь степень $V=8$ которая максимально.

Лемма 1: в графе $G$ с тремя последовательными вершинами со степенями $A(8)$ может быть в сумме не больше $4$ .

Доказательство: Возьмем вершину $A_{1}$ без о.о пусть из нее проведены $k$ красных и $8-k$ синих отрезков, тогда тогда из вершины $A_{2}$ однозначно закрашиваются в $k-1$ синих отрезков (чтобы не образовался треугольник) тогда как минимум $k-1$ вершин имеются степень не $8$, значит могут иметь $9-(k-1)=10-k$ вершин могут иметь степень $8$.

случай $1$ если из $A_{1}$ и соседние с ним $A_{2},A_{9}$ имеют разные цвета, то из них же однозначно проводятся отрезки $k-1$ c cиних и $8-k-1=7-k$ красных соответственно, значит $A(8) \leq 10-(k-1+7-k)=3$ вершины имеют степень $8$

случаи $2$ если из $A_{1}$ и соседние с ним $A_{2},A_{9}$ имеют одинаковые цвета к примеру синие, а остальные красные, тогда для $6$ остальных максимум $10-6=4$ вершины имеют степень $8$.

Тогда из леммы 1 получается для двух последовательных вершин со степенью $8$, вершин со степенью $8$ может быть в сумме не больше $4$, так как к примеру

если из вершины проведены $k$ красных и $8-k$ синих, то в сумме отрезков будет не больше чем $9-(k-1+8-k-1) = 3$ исключение составляет когда $k=6$ так для него $8-6=2$ вершин могут быть соединены вершинами со степенью $8$ и того $9-(6-1)=4$

Так же отметим что какие то две вершины всегда будут иметь степень не больше $7$ так как найдется треугольник с вершинами в которых не может быть степень $8$, так как их всегда больше $3$ следую из рассуждений, тогда получаем из каждой вершины этого треугольника не могут быт проведены как минимум два отрезка, то есть степень их не больше $7$, значит $66$ в сумме получится не может.