34-я Международная Математическая OлимпиадаТурция, Стамбул, 1993 год

Дан остроугольный треугольник $ABC$ и точка $D$ внутри него такая, что $\angle ABC=\angle ACB+90{}^\circ $ и $AC\cdot BD=AD\cdot BC$.
а) Вычислить значение отношения $\dfrac{AB\cdot CD}{AC\cdot BD}$.
б) Доказать, что касательные, проведенные в точке $C$ к окружностям, описанным около треугольников $ACD$ и $BCD$, перпендикулярны.

Комментарий/решение

Если имелось ввиду $\angle ADB = \angle ACB +90^{\circ}$ иначе ответ в $a$ неоднозначный.

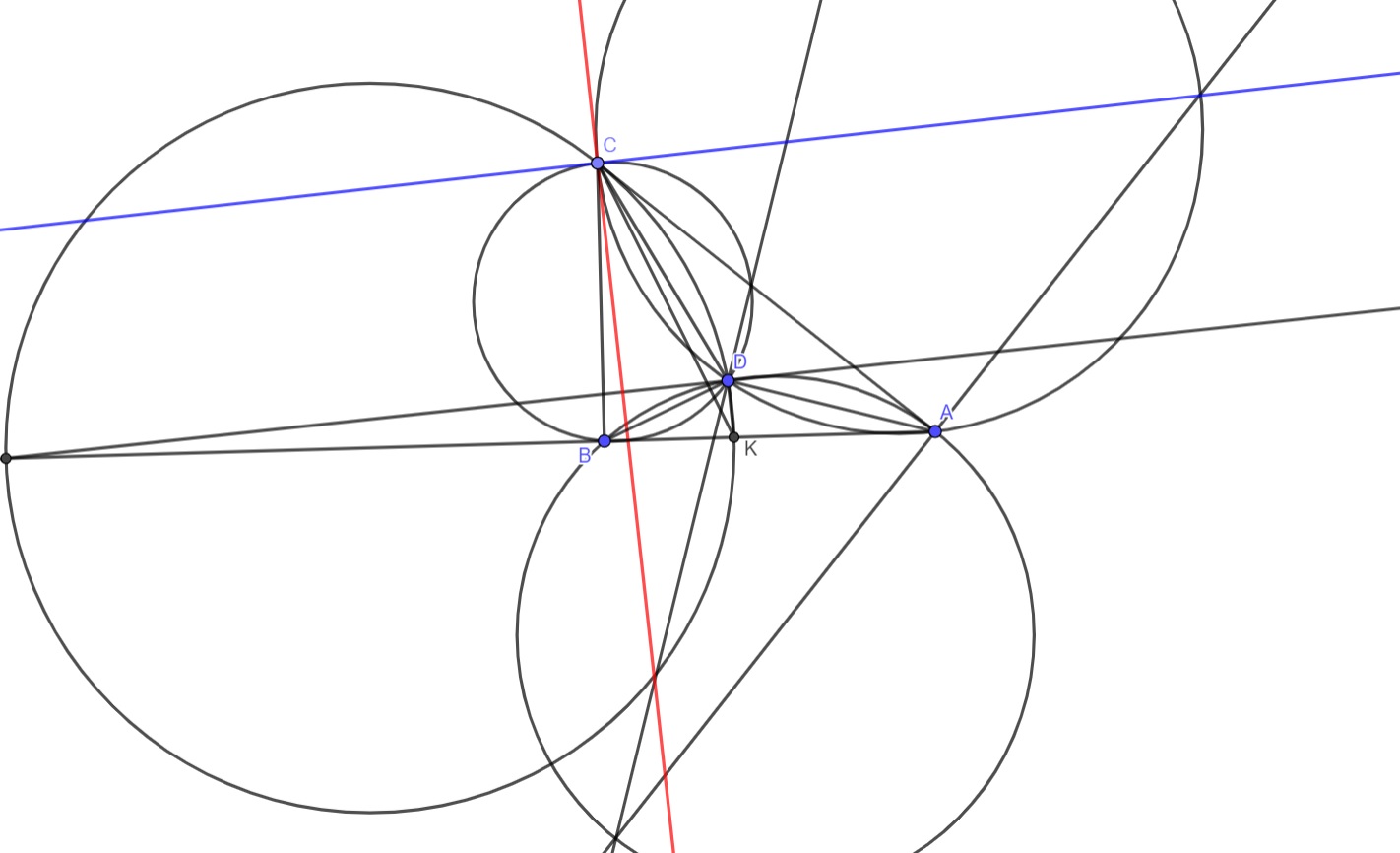
Рассмотрим некоторый треугольник $ADB$ проведем биссектрису $DK$ построим перпендикуляр $l$ к $DK$ пусть $N \in l \cap AB$ построим окружность $\omega$ как на диаметре $NK$ возьмем на $\omega$ произвольную точку $C$ тогда по построению $\dfrac{AC}{BC} = \dfrac{AD}{BD}$ ($\omega$ есть окружность Аполлония для точек $A,B$)

Лемма: выше приведенном построении выполняется условие:

$\dfrac{AB}{BC} \cdot \dfrac{CD}{AD} = 2\sin( \angle BDK - \angle BCK) $

Доказательство: Пусть $\angle BDK=a ,\ \angle BAD=b, \angle ABC=c, \angle BCK=x, \angle DCK=90^{\circ}-a-b$

Тогда лемма после выражения из треугольников $ABC, ADC$ и преобразований будет иметь вид

$\sin(\angle 2a) \cdot \sin(c+2a+b) = 2 \sin(a-x) \cdot \cos(x+c+a) \cdot \sin(2a+b) $

а это и есть Теорема Чевы для треугольника $ABC$ и точки $D$ записанной в угловой форме.

a) Тогда из условия $\angle ABC=90^{\circ} + \angle ACB$ выходит

$\dfrac{AB}{BC} \cdot \dfrac{CD}{AD} = 2\sin( \angle BDK - \angle BCK) = 2\sin(\dfrac{ \angle ABC - \angle ACB}{2}) = 2\sin(45^{\circ}) = \sqrt{2} $

значит $\dfrac{AB \cdot CD}{AC \cdot BD} = \sqrt{2}$

б) Непосредственно следует из условия $\angle 2a = \angle 2x +90^{\circ}$ то есть

Проведя касательные, угол между ними $\angle DAC+\angle DBC=180^{\circ}-c-2x-b+c-(180^{\circ}-2a-b) = 2a-2x = 90^{\circ}$