37-я Международная Математическая OлимпиадаИндия, Мумбаи, 1996 год

Пусть $ABCDEF$ — выпуклый шестиугольник такой, что $AB\parallel ED$, $BC\parallel FE$ и $CD\parallel AF$. Обозначим через ${{R}_{A}}$, ${{R}_{C}}$, ${{R}_{E}}$ радиусы окружностей, описанных около треугольников $FAB$, $BCD$, $DEF$ соответственно, а через $P$ — периметр шестиугольника. Доказать, что ${{R}_{A}}+{{R}_{C}}+{{R}_{E}}\ge P/2$.

Комментарий/решение

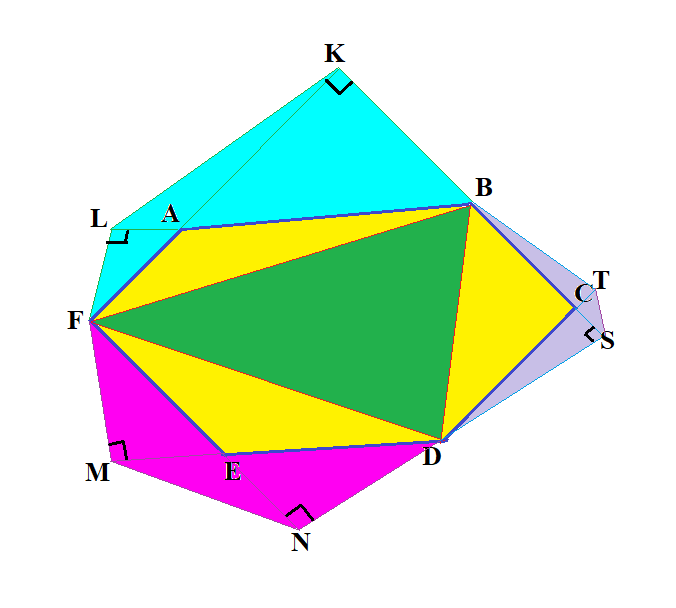
$$ \angle BAF=\alpha\Rightarrow \angle LAF = \pi -\alpha \quad \angle FED=\beta \Rightarrow \angle MEN=\pi-\beta \quad \angle BCD= \gamma \Rightarrow \angle DCS=\pi-\gamma$$

$$ FL \perp AL \Rightarrow AL=AF\cos(\pi-\alpha)=-AF\cos\alpha\Rightarrow LF=AF\sin\alpha\Rightarrow $$

$$ KB\perp AK \Rightarrow AK=AB\cos(\pi-\alpha)=-AB\cos\alpha\Rightarrow BK=AB\sin\alpha$$

$$ KL=\sqrt{AL^2+AK^2-2AL\cdot AK \cos \alpha}=\sqrt{AF^2\cos^2\alpha+AB^2\cos^2\alpha-2AB\cdot AF\cos^3\alpha}=$$

$$= |\cos\alpha|\sqrt{AF^2+AB^2-2AB\cdot AF\cos\alpha}=BF|\cos\alpha|\Rightarrow KL \leq BF$$

$$LF+BK=(AF+AB)\sin\alpha\leq BF \Rightarrow AF+AB\leq \frac{BF}{\sin\alpha}=\frac{BF \cdot AB\cdot AF}{AB\cdot AF\sin\alpha}\Rightarrow$$

$$\Rightarrow \frac{AF+AB}{2}\leq \frac{BF \cdot AB\cdot AF}{2AB\cdot AF\sin\alpha}=\frac{BF \cdot AB\cdot AF}{4\cdot \frac{1}{2}AB\cdot AF\sin\alpha}=\frac{BF \cdot AB\cdot AF}{4\cdot S_{\triangle ABF}}=R_A\Rightarrow$$

$$\Rightarrow \frac{AF+AB}{2}\leq R_A$$

Точно также получаем

$$\frac{BC+CD}{2}\leq R_C$$

$$\frac{EF+ED}{2}\leq R_E$$

Теперь, складывая все эти неравенства, имеем

$$\frac{AB+BC+CD+DE+EF+FA}{2}=\frac{P}{2}\leq R_A+R_E+R_C$$