50-я Международная Математическая Oлимпиада
Германия, Бремен, 2009 год
Комментарий/решение:
Из условия следует что $M$ - точка касания, тогда $DM \perp QP$ где $D$ - центр описанной окружности $KLM$, проведем до пересечения $QP$ с описанной окружностью , пусть она пересекает ее в точках $E,F$, так же отметим что $\angle KML = \angle PAQ $ (из -за параллельности) и $\angle MKL = \angle PML = \angle APQ$ то есть $MKL, APQ$ подобны значит $\dfrac{AP}{AQ} = \dfrac{MK}{ML}$ значит $AP \cdot ML=AQ \cdot MK$ домножим на $2$ и учитывая что $ML, MK$ средние линии $PQC, BPQ$ откуда $AP \cdot PC = AQ \cdot BQ$ но с другой стороны $AP \cdot PC = (EQ+PQ) \cdot PF$ и $ AQ \cdot BQ = EQ \cdot (PF + PQ)$ откуда $(EQ+PQ) \cdot PF = EQ \cdot (PF+PQ)$ значит $EQ = PF$ откуда следствии равенство треугольников $EQO, PFO$ получаем $OP=OQ$.
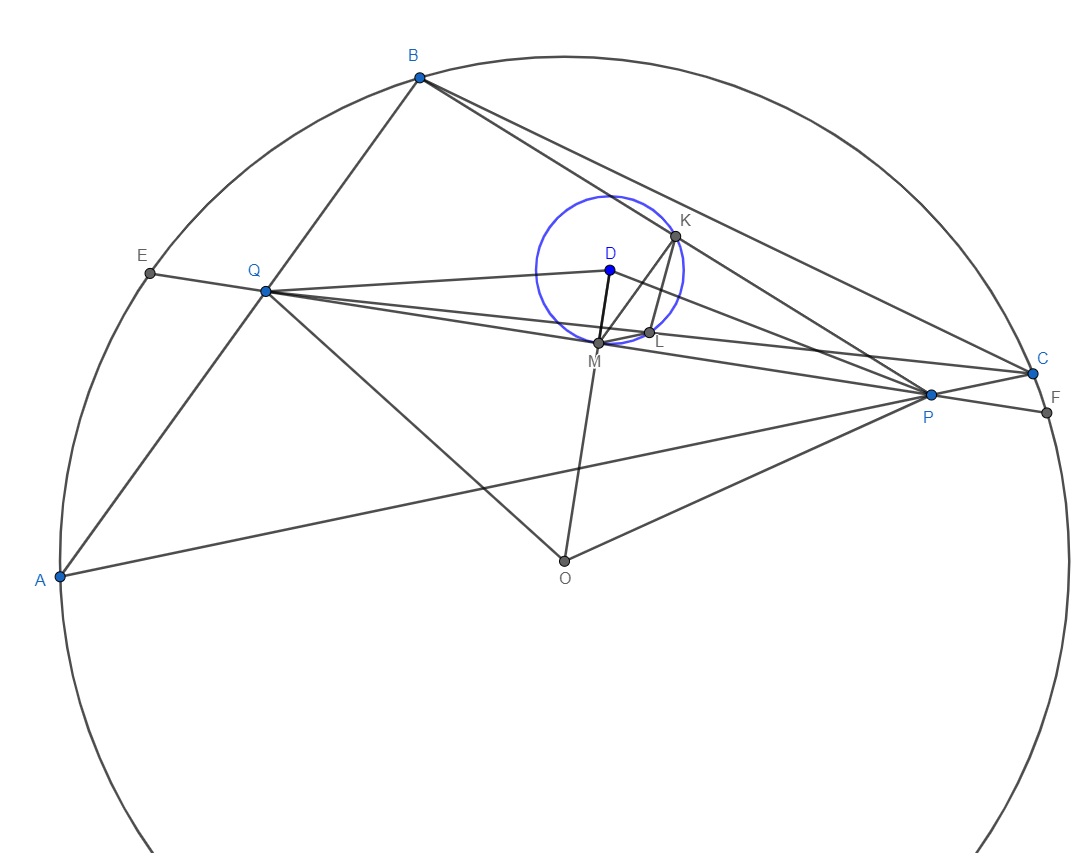
Заметим, что $$ML\parallel PC,\quad 2ML=PC$$ $$MK\parallel QB,\quad 2MK=QB$$
Так как $Γ$ касается $PQ$, то $$\angle MKL=\angle PML=\angle APQ$$ второе равенство следует из $ML\parallel PC$, значит $$\angle MKL=\angle APQ$$ Аналогично $$\angle MLK=\angle AQP$$ Из двух последних равенств получаем, что $$\triangle MLK\sim \triangle AQP$$
Следовательно $$\frac {ML}{AQ}=\frac{MK}{AP}\implies 2ML×AP=2MK×AQ$$ $$\implies AP×PC=AQ×QB$$ Поэтому $$Pow_ω(P)=Pow_ω(Q)$$ где $ω$ $-$ описанная окружность $\triangle ABC$, а $Pow_ω(X)$ $-$ степень точки $X$ относительно окружности $ω$.
Тогда $OP^2=Pow_ω(P)+R^2=Pow_ω(Q)+R^2=OQ^2\implies OP=OQ$ , где $R$ $-$ радиус окружности $ω$.

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.