Районная олимпиада, 2005-2006 учебный год, 8 класс

На сторонах $AC$ и $BC$ остроугольного треугольника $ABC$ выбраны соответственно точки $D$ и $E$ так, что $AD:DC=3:4$ и $BE:EC=2:3$. Найдите $\frac{AF\cdot BF}{FE\cdot FD}$, где $F$ — точка пересечения $AE$ и $BD$.

Комментарий/решение

Ответ: $\dfrac{35}{12}$

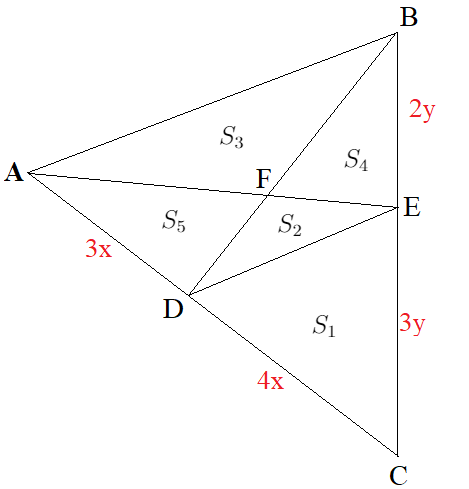
$$ S_1+S_2+S_3+S_4+S_5=S$$

$$ \frac{S_1}{S}=\frac{\frac{1}{2}EC \cdot CD \sin\angle BAC}{\frac{1}{2}BC \cdot CA \sin\angle BAC}=\frac{12xy}{35xy}=\frac{12}{35}$$

$$ \frac{S_1+S_2+S_5}{S}=\frac{\frac{1}{2}EC \cdot CA \sin\angle BAC}{\frac{1}{2}BC \cdot CA \sin\angle BAC}=\frac{21xy}{35xy}=\frac{21}{35}\Rightarrow \frac{S_2+S_5}{S}=\frac{9}{35}$$

$$ \frac{S_3+S_4}{S}=\frac{14}{35}$$

$$ S_2\cdot S_3=S_4\cdot S_5 $$

$$ S_2S_3+S_2S_4=S_4S_5+S_2S_4 \Rightarrow S_2\left(\frac{S_3+S_4}{S}\right)=S_4\left(\frac{S_2+S_5}{S}\right) \Rightarrow $$

$$ \Rightarrow S_2=\frac{9}{14}S_4 $$

$$\left\{ \begin{gathered} \frac{14}{9}S_2+S_3=\frac{14}{35}S\\ S_3-S_2=\frac{6}{35}S \\ \end{gathered} \right.\Rightarrow \frac{35}{3}S_2=4S_3\Rightarrow \frac{S_3}{S_2}=\frac{AF \cdot BF}{FE \cdot FD}=\frac{35}{12}$$

Задача легко решается через теорему Менелая: $\dfrac{BE}{BC} \cdot \dfrac{CD}{DA} \cdot \dfrac{AF}{FE}=1, \Rightarrow \dfrac{AF}{FE}=15/8,$ аналогично $\dfrac{BF}{FD}=14/9$, тогда ответ:$35/12$