Районная олимпиада, 2004-2005 учебный год, 8 класс

Диагонали трапеции равны 6 см и 8 см, а отрезок, соединяющий середины ее оснований, равен 5 см. Найдите площадь трапеции.

Комментарий/решение

Пусть основания трапеции -$AD, BC$;точка пересечения диагоналей -$E$, середина $BC$-точка$F$, середина $AD$-точка $G$. Воспользуюсь теоремой о трапеции, по которой линия, соединяющая середины оснований и диагонали пересекаются в одной точке. Кроме того, треугольники $BCE$ и $DAE$ подобные по трем углам. Пусть $BE=b; FE=x; CE=a$ , тогда $EG=5-x; ED=8-b; AE=6-a$. Из подобия треугольников $BCE$ и $DAE$ получим$$\dfrac{a}{6-a}=\dfrac{b}{6-b}$$,откуда $a=\dfrac{3b}{4} $. Из подобия треугольников $BFE$ и $DGE$ получим $\dfrac{x}{b}=\dfrac{5-x}{8-b}$ ,откуда $x=\ dfrac{5b}{8} $. Продлим треугольник $BEC$ до параллелограмма $BHCE$. У параллелограма сумма кадратов диагоналей равна сумме квадратов сторон, поэтому $EH^2+BC^2=2 (BE^2+EC^2) $. Или $(\dfrac{5b}{4})^2+BC^2=2 (b^2+\dfrac{9b^2}{16}) $,откуда $BC^2=\dfrac{25b^2}{16}$. В то же время по теореме косинусов из треугольника $BEC$ получим $cosBEC=\dfrac{BE^2+EC^2-BC^2}{2BE*EC}=\dfrac{b^2+\dfrac{9b^2}{16}-\dfrac{25b^2}{16} }{2b*3b/4} =0$, откуда $\sin(BEC)=1$. Из этого $ S_{ABCD}=(d1*d2*sinBEC)/2=\dfrac{6×8×1}{2}=24$

Ответ: 24

Так как в Казахстане тригонометрию проходят в конце 8-класса, хочу поделиться решением без тригонометрии:

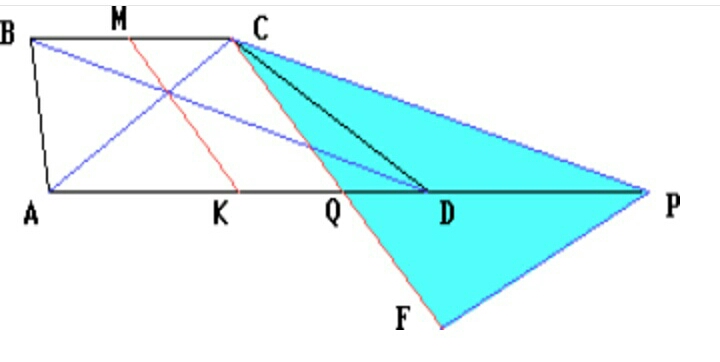
Пусть $M$ и $K$ — середины оснований $BC$ и $AD$ трапеции $ABCD$. Через вершину $C$ меньшего основания $BC$ $(AC = 6, BD = 8)$ проведём прямую, параллельную диагонали $BD$, до пересечения с прямой $AD$ в точке $P$ и прямую, параллельную $MK$, до пересечения с прямой $AD$ в точке $Q$. Тогда $AQ = AK + KQ = AK + MC = AD/2 + BC/2 =$ $=(AD + BC)/2 = (AD + DP)/2.$

Поэтому $CQ$ — медиана треугольника $ACP$, $CQ = MK = 5,$ $AC = 6,$ $CP = BD = 8,$ $S_{ABCD}= S_{\Delta ACP}$.

На продолжении медианы $CQ$ за точку $Q$ отложим отрезок $QF,$ равный $CQ.$ Стороны треугольника $CFP$ равны: $CF = 2CQ = 10,$ $CP = BD = 8,$ $FP = AC = 6.$ Этот треугольник прямоугольный ($CF^2 = CP^2 + PF^2$). Поэтому $S_{\Delta CFP} =CP\cdot PF/2 = 24.$ Следовательно, $S_{ABCD} = S_{\Delta ACP} = S_{\Delta CFP} = 24.$