Городская олимпиада по математике среди физ-мат школ г. Алматы, 2015 год

Высоты $AA_1$ и $CC_1$, остроугольного треугольника $ABC$ пересекаются в точке $H$. На высоте $AA_1$ отмечена точка $P$ такая, что $A_1P=AH$, на высоте $CC_1$, отмечена точка $Q$ такая, что $C_1Q=CH$. Докажите, что перпендикуляры к прямым $AA_1$ и $CC_1$, проходящие через точки $P$ и $Q$ соответственно, пересекаются на описанной окружности треугольника $ABC$. ( Ильясов С. )

Комментарий/решение

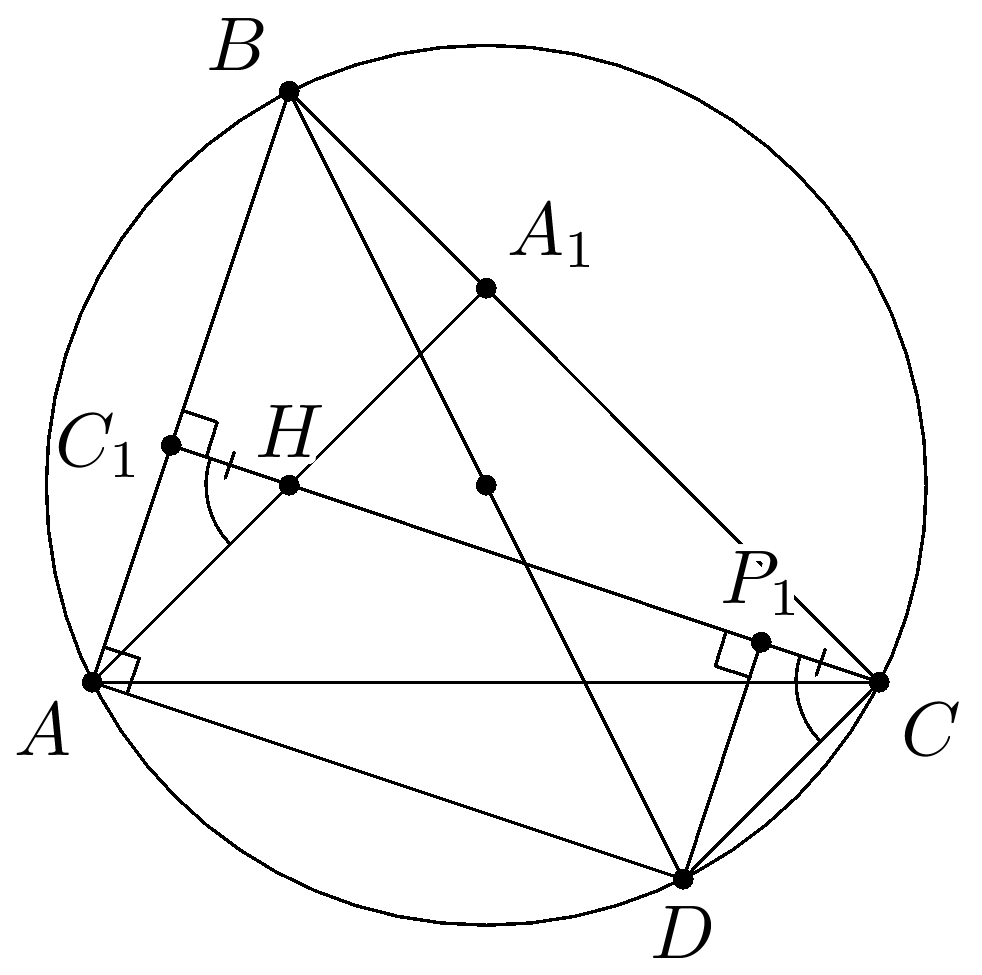
Комментарии от администратора Комментарии от администратора №1.     Понятно, что точка $H$ лежит внутри треугольника и углы $\angle {{C}_{1}}B{{A}_{1}}=\angle {{C}_{1}}HA$ острые. Пусть $BD$ --- диаметр описанной окружности. Докажем, что данные прямые пересекаются в точке $D$. Так как $AD\bot AB$ и $CH\bot AB$, то $AD\parallel CH$. Аналогично, $DC\parallel AH$. Следовательно, $ADCH$ --- параллелограмм. Опустим перпендикуляр $D{{P}_{1}}$ на прямую $C{{C}_{1}}$. Так как $AH=CD$, $\angle AH{{C}_{1}}=\angle DC{{P}_{1}}$, то прямоугольные треугольники $AH{{C}_{1}}$ и $DCP$ равны и точка ${{P}_{1}}$ лежит на отрезке $CH$. Значит, ${{C}_{1}}H=C{{P}_{1}}$ т.е. точки ${{P}_{1}}$ и $P$ совпадают. Это говорит о том, что перпендикуляр к прямой $A{{A}_{1}}$ в точке $P$ проходит через $D$. Аналогично, перпендикуляр к прямой $C{{C}_{1}}$ в точке $Q$ также проходит через $D$.