Республиканская олимпиада по математике, 2016 год, 9 класс
Клетчатую таблицу $n \times n$ (где $n \geq 2$) покрывают уголками, состоящими из трёх единичных клеток (уголок можно неоднократно поворачивать на $90{}^\circ $) так, чтобы выполнялись следующие условия:
1) каждая клетка таблицы покрыта хотя бы одним из уголков;
2) две соседние по стороне клетки, покрытые одним уголком, не могут быть одновременно покрыты другим.
Каково наибольшее возможное число уголков в таком покрытии? ( Ильясов С. )
посмотреть в олимпиаде
1) каждая клетка таблицы покрыта хотя бы одним из уголков;
2) две соседние по стороне клетки, покрытые одним уголком, не могут быть одновременно покрыты другим.
Каково наибольшее возможное число уголков в таком покрытии? ( Ильясов С. )
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1.
Ответ. $n(n-1)$.
Будем рассматривать каждый уголок в виде наложения двух доминошек: горизонтального и вертикального (см. рис. ниже).
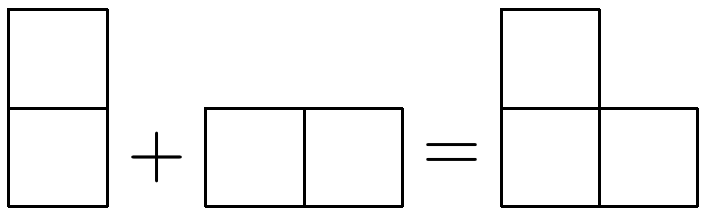
Тогда можно считать, что таблица покрыта доминошкоми по следующим двум правилам:
1) каждая клетка таблицы покрыта хотя бы одной доминошкой.
2) никакая доминошка полностью не покрывает никакую другую.
При таком условии каждая строка или столбец длины $n$ покрываются не более чем $n-1$ доминошкой $2 \times 1$ или $1 \times 2$ соответственно. Поэтому всего доминошек не более чем $2n(n-1)$. Но каждому уголку соответствует $2$ доминошки, поэтому число уголков не более чем $n(n-1)$.
Пример. Строить пример будем по индукции с шагом два.
1) Когда $n=2$ и $n=3$ привести не трудно.
2) Пусть для каждого $k \leq n$ мы показали.
3) Покажем для $k=n+2$.
Рассмотрим ободок ширины 2, полученный из таблицы ${(n+2)}\times{(n+2)}$ путем вырезания центрального квадрата ${(n-2)}\times{(n-2)}$. Поставим уголок (такой как на рис. выше) в нижний левый угол, назовем его первым. Затем переместим его на одну клетку вверх, в новом месте поставим такой же уголок и т.д. В итоге левая часть ободка покрыта ${n+1}$ уголками. Затем переместим первый уголок на одну клетку вправо,в новом месте поставим такой же уголок и т.д. В итоге левая и нижняя часть ободка покрыты ${2n+1}$ уголками. Повернем ободок на $180^\circ $ и проделаем ту же операцию. Таким образом ободок покрыт ${4n+2}$ уголками.
Заметим, что каждый такой уголок покрывает не более одной клетки из центрального квадрата $n \times n$, это означает, что никакой уголок полностью лежащий в центральном квадрате $n \times n$, не противоречит условиям покрытия. Значит в силу предположения индукции центральный квадрат покрывается $n^2-n$ уголками, т.е. таблицу ${(n+2}) \times{( n+2})$ покрыта $n^2-n+4n+2 = n^2 + 3n +2 ={(n+2)}\cdot{(n+1)}$ уголками.

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.