Республиканская олимпиада по математике, 2016 год, 10 класс

Вписанная окружность треугольника $ABC$ касается сторон $BC$ и $AC$ в точках $A_1$ и $B_1$, а вневписанная окружность, соответствующая стороне $AB$, касается продолжении этих сторон в точках $A_2$ и $B_2$ соответственно. Пусть вписанная в $\triangle ABC$ окружность касается стороны $AB$ в точке $K$. Обозначим через $O_a$ и $O_b$ центры описанных около треугольников $A_1A_2K$ и $B_1B_2K$ окружностей. Докажите, что прямая $O_aO_b$ проходит через середину отрезка $AB$. ( М. Кунгожин )

Комментарий/решение

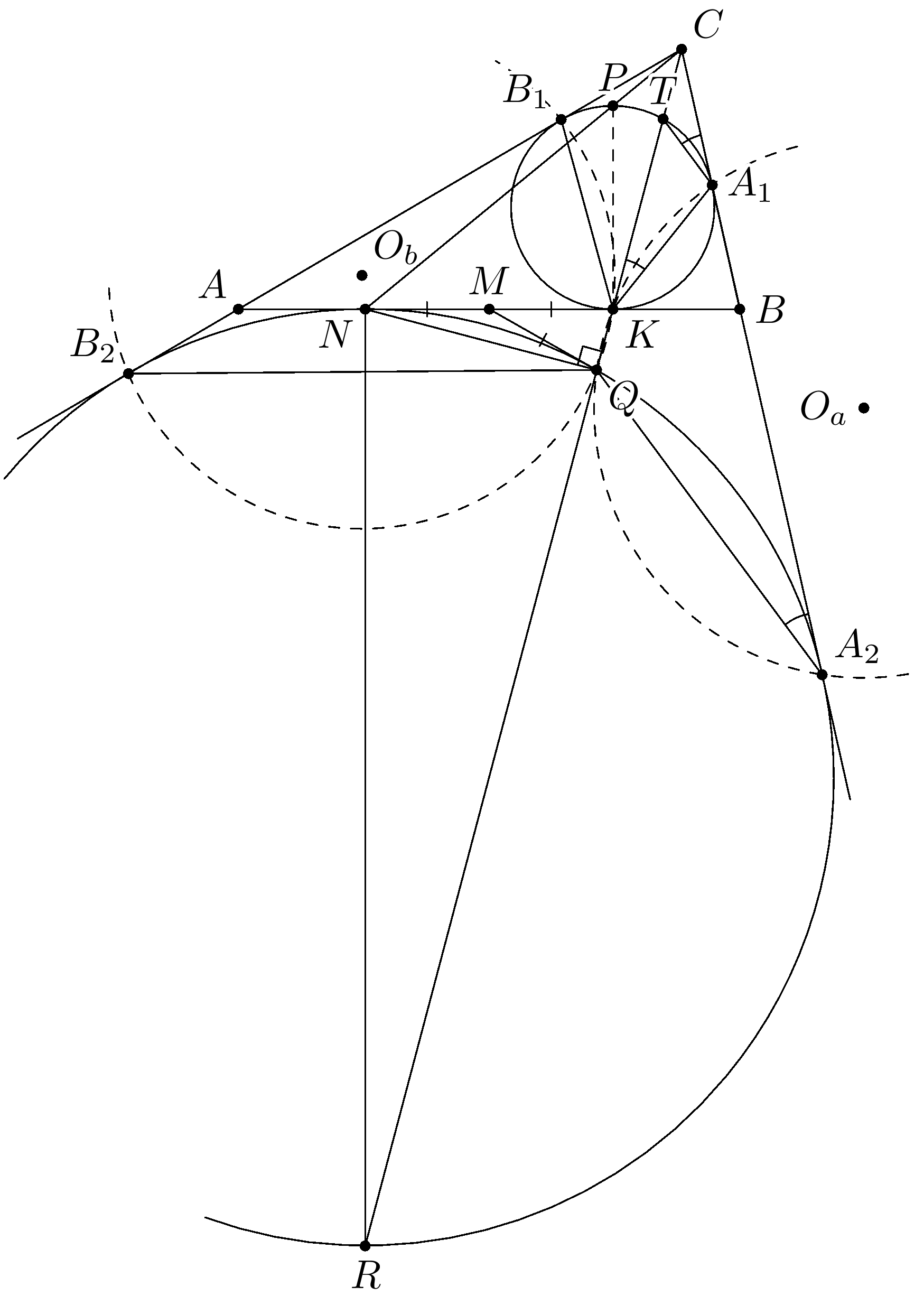
Комментарии от администратора Комментарии от администратора №1.     Обозначим вписанную и вневписанную окружности через $\omega_1$ и $\omega_2$ соответственно. Пусть $\omega_2$ касается стороны $AB$ в точке $N$, а $KP$ и $NR$ — диаметры $\omega_1$ и $\omega_2$ соответственно. Понятно, что точка $C$ является центром гомотетии, переводящий $\omega_1$ в $\omega_2$. Тогда при этой гомотетии точка $P$ перейдет в точку $N$, а точка $K$ в точку $R$. Обозначим вторые точки пересечения прямой $CR$ с окружностями $\omega_1$ и $\omega_2$ через $T$ и $R$ соответственно. При рассматриваемой гомотетии точке $T$ соответствует точка $Q$, а точке $A_1$ — точка $A_2$. Следовательно, $\angle QA_2C = \angle TA_1C = \angle TKA_1$, то есть четырехугольник $A_1KQA_2$ вписанный. Аналогично, четырехугольник $B_1KQB_2$ также вписанный. Следовательно, для этих описанных окружностей $KQ$ является общей хордой, поэтому $O_aO_b$ лежит на серединном перпендикуляре отрезка $KQ$. Обозначим середину отрезка $AB$ через $M$. Тогда, для решения задачи, достаточно показать, что $M$ также лежит на серединном перпендикуляре отрезка $KQ$. Здесь можно сразу воспользоваться тем фактом, что $N$ и $K$ симметричны друг другу относительно $M$. И, так как $NR$ является диаметром $\omega_2$, то треугольник $NQK$ прямоугольный, $MK=MQ$, то есть $M$ также лежит на серединном перпендикуляре отрезка $KQ$.