Республиканская олимпиада по математике, 2017 год, 9 класс


На сторонах треугольника $ABC$ во внешнюю сторону построены прямоугольники равных площадей $ABLK$, $BCNM$ и $CAQP$. Пусть $X$, $Y$ и $Z$ середины отрезков $KQ$, $LM$ и $NP$ соответственно. Докажите, что прямые $AX$, $BY$ и $CZ$ пересекаются в одной точке. ( М. Кунгожин )
посмотреть в олимпиаде

Комментарий/решение:

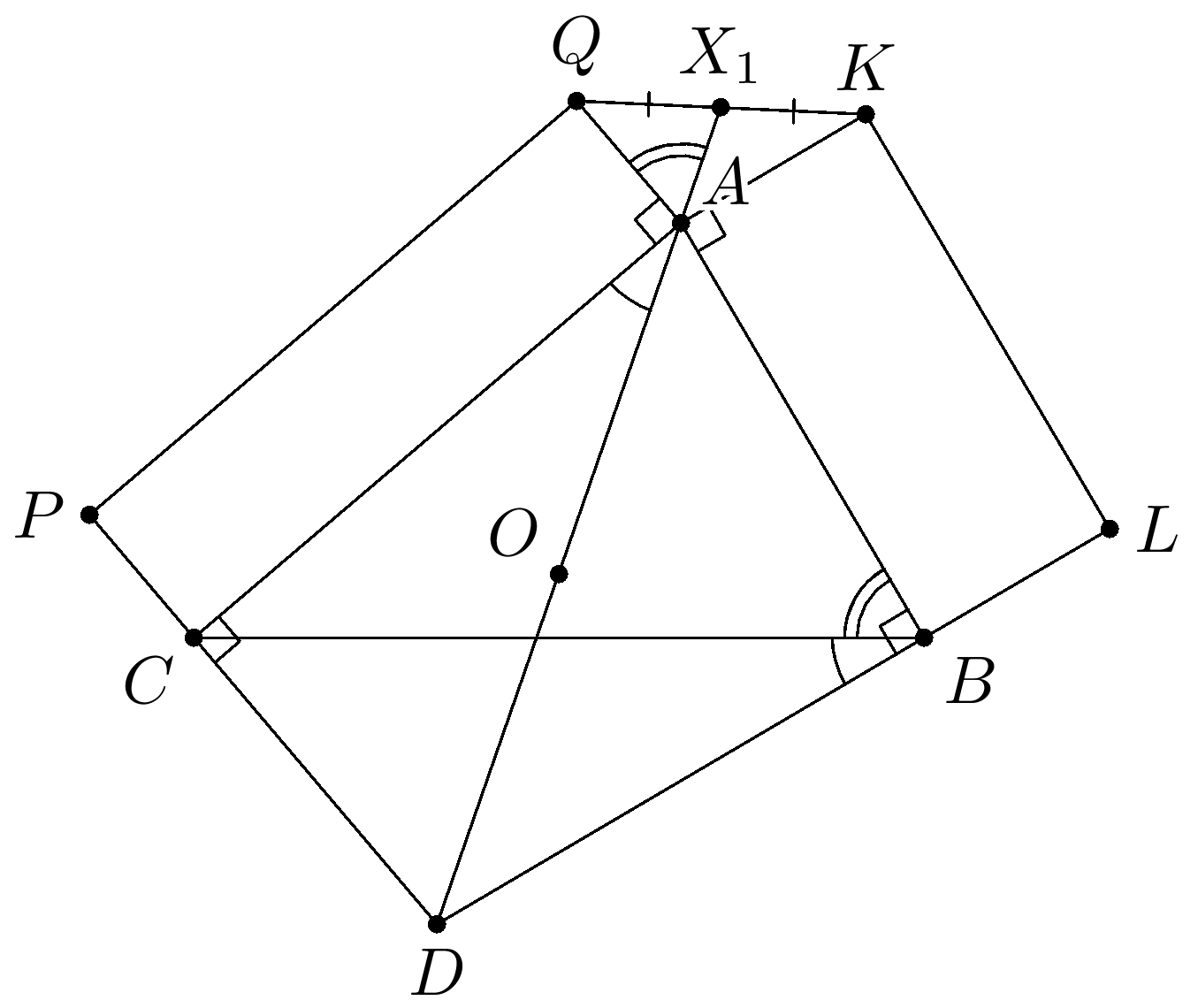
Комментарии от администратора Комментарии от администратора №1.     Решение. Пусть стороны треугольника $ABC$ имеют фиксированные стороны. Заметим, что если не фиксированные стороны прямоугольников увеличивать пропорционально, то прямые $AX,BY$ и $CZ$ будут постоянными. Следовательно, эти прямые проходят через какую-то фиксированную точку треугольника. Пусть точка $O$ — центр описанной окружности треугольника $ABC$. Докажем, что $O$ — искомая точка.

Обозначим $D=CP \cap BL$. Тогда точки $A,B,C,D$ лежат на одной окружности с диаметром $AD$; также на этом диаметре лежит точка $O$. Пусть $X_1=AD \cap KQ$. Так как $\angle CAD = \angle CBD$ и $$\angle CAD + \angle QAX_1= \angle CBD + \angle ABC = 90^\circ,$$ то $\angle QAX_1=\angle ABC$. Аналогично, $\angle KAX_1 = \angle ACB$. Пусть прямоугольники имеют площадь $S$. Тогда, $$\frac{QX_1}{KX_1}=\frac{AQ}{AK} \cdot \frac{\sin QAX_1}{\sin KAX_1} = \frac{S/AC}{S/AB} \cdot \frac{\sin ABC}{\sin ACB} =\frac{AB}{AC} \cdot \frac{AC}{AB}=1,$$ то есть $X_1$ — середина отрезка $QK$ или $X_1$ совпадает с $X$. Следовательно, прямая $AX$ проходит через точку $O$. Аналогичное утверждение можно доказать для прямых $BY$ и $CZ$.

  0
2024-09-23 20:45:45.0 #

Лемма:

На сторонах $AB,AC$ треугольника $ABC$ построены квадраты $ABPX$ и $ACQY$. Тогда верно, что высота $\triangle ABC$ в точке $A$ является медианой $\triangle AXY$.

Построим из задачи прямоугольники с площадью $S=AB\cdot AC$. Тогда верно, что $ACPQ$ и $ABLK$ отличаются поворотом. Треугольник из леммы отличается от треугольника $AKQ$ симметрией относительно общей биссектрисы $\angle BAC$ и $\angle QAK$. Поэтому $AX$ - изогональ к высоте $\triangle ABC$ в точке $A$. Поэтому задача решена, так как линейное движение точек прямоугольника линейно передвигает и точки $X,Y,Z$.

ImaRHB