Республиканская олимпиада по математике, 2017 год, 9 класс

Неравнобедренный треугольник $ABC$ вписан в окружность $\omega$ с центром $O$. Продолжение биссектрисы $CN$ пересекает $\omega$ в точке $M$. Пусть $MK$ — высота треугольника $BCM$, $P$ — середина отрезка $CM$, а $Q$ — точка пересечения прямых $OP$ и $AB$. Пусть прямая $MQ$ во второй раз пересекает $\omega$ в точке $R$, а $T$ — точка пересечения прямых $BR$ и $MK$. Докажите, что $NT \parallel PK$. ( М. Кунгожин )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Решение. Рассмотрим случай, когда $AC > BC$. Остальные случаи разбираются аналогично. Прямоугольные треугольники $OPM$ и $BKM$ подобны, так как $\angle POM=\angle CAM=\angle KBM$. В треугольнике $OMQ$ точка $N$ является его точкой пересечения высот. Поэтому $\angle PON=\angle NMQ=\angle CBR=\angle TBK$, то есть $ON$ и $BT$ являются соответствующими в этих подобных треугольниках $OPM$ и $BKM$. Следовательно, $MN/NP=MT/TK$ или $NT\parallel PK$.

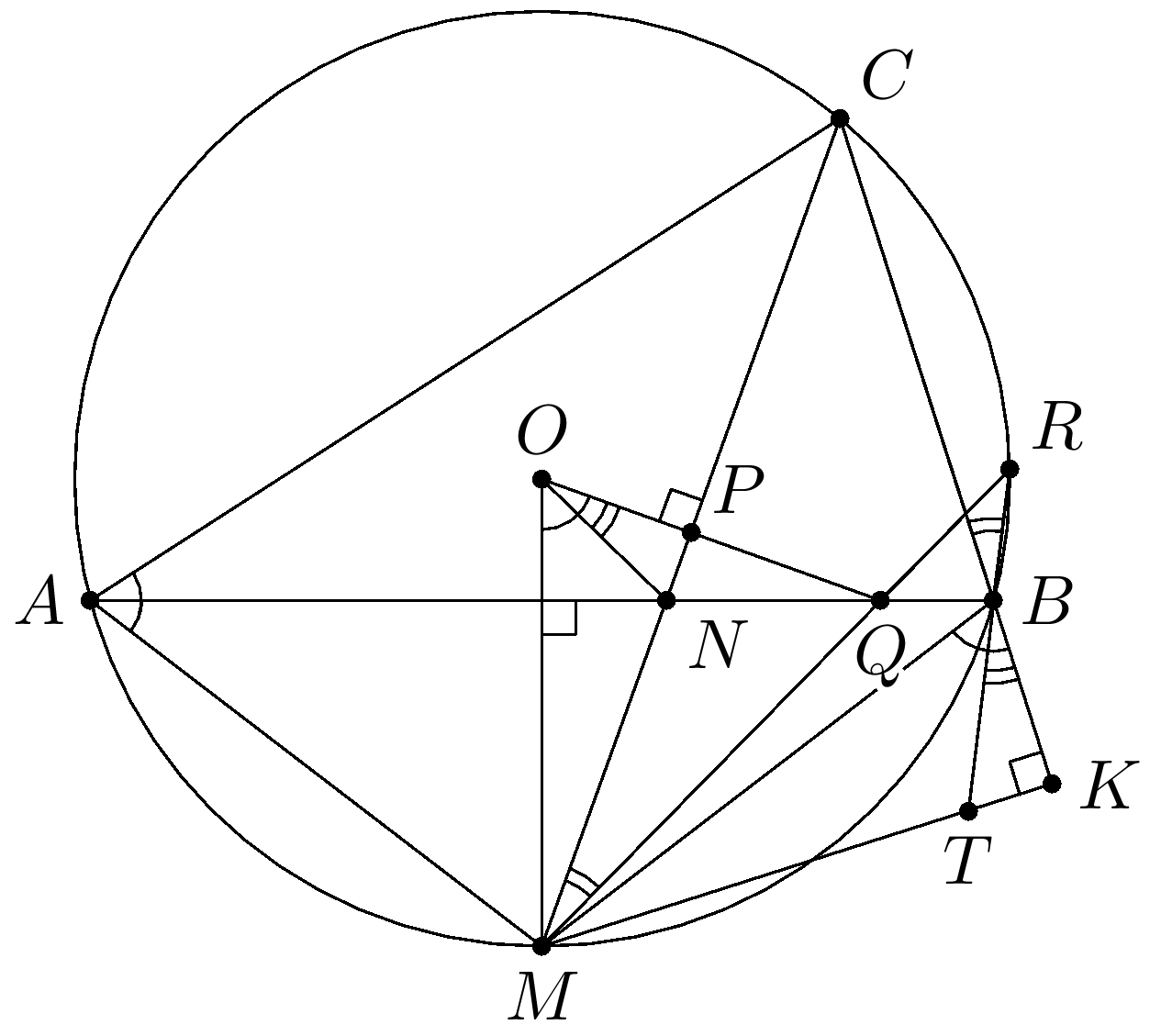
(Респа Камп, 8 февраля) Пусть $CA < CB$ и $S$ такая точка на прямой $CB$, что $\angle SMK = \angle CMQ,$ тогда треугольники $MPQ$ и $MKS$ подобны. $\angle CMQ = \angle CBR = \angle SMK,$ значит $BTMS$ вписанный. $\angle KST = \angle BMT = 90^{\circ} - \angle KBM = \angle PQN$ (легко считаются), откуда $N$ и $T$ соответствующие точки в подобных треугольниках $MPQ$ и $MKS,$ а значит $\dfrac{MN}{NP} = \dfrac{MT}{TK}$ ч.т.д.

Балама дәлелдеуі:

1) $NT \parallel PK$ болсын деп ұйғарайық. $CP = MP = KP$, ендеше $\triangle KPC$ әрі $\triangle KPM$ тең бүйірлі болады.

2) Белгілеу еңгізейік $\angle MCK = \alpha$, олай болса $\angle KPC = 180 - 2\alpha$, $\angle KPM = 2\alpha$, ал $\angle PMK = \angle PKM = 90 - \alpha$.

3) Ұйғарым бойынша $NT \parallel PK$, демек $\triangle MNT$ да тең бүйірлі, яғни $\triangle MNT$ мен $\triangle MPK$ ұқсас болады, ендеше $\angle NMT = \angle NTM = 90 - \alpha$ және $\angle MNT = 2\alpha$. Сонымен, жасалған ұйғарым дұрыс екен, яғни $NT \parallel PK$ д.к.о.е.