Республиканская олимпиада по математике, 2017 год, 10 класс


Дан неравнобедренный треугольник $ABC$. Точки $K$ и $N$ лежат на стороне $AC$, а точки $M$ и $L$ на стороне $BC$ так, что $AN=CK=CL=BM.$ Пусть отрезки $KL$ и $MN$ пересекаются в точке $P$. Докажите, что $\angle RPN = \angle QPK$, где $R$ — середина стороны $AB$, а $Q$ — середина дуги $ACB$ окружности, описанной около треугольника $ABC$. ( М. Кунгожин )
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.     Решение. Без потери общности положим $AC > BC$. Обозначим $MN \cap AB=X$, $KL \cap AB=Y$. Применим два раза теорему Менелая для треугольника $ABC$ и его секущих $MX$ и $KY$. Имеем: $$\frac{BX}{AX}\cdot \frac{AN}{NC} \cdot \frac{CM}{MB}=1 = \frac{AY}{BY} \cdot \frac{BL}{LC} \cdot \frac{CK}{KA}.$$ Так как $AN=CK$, $NC=KA$, $CM=BL$ и $MB=LC$, то $BX/AX=AY/BY$, откуда $AX=BY$ или точки $X$ и $Y$ симметричны относительно $R$. Так как обе точки $R$ и $Q$ лежат на серединном перпендикуляре отрезка $AB$, то треугольник $QXY$ равнобедренный.

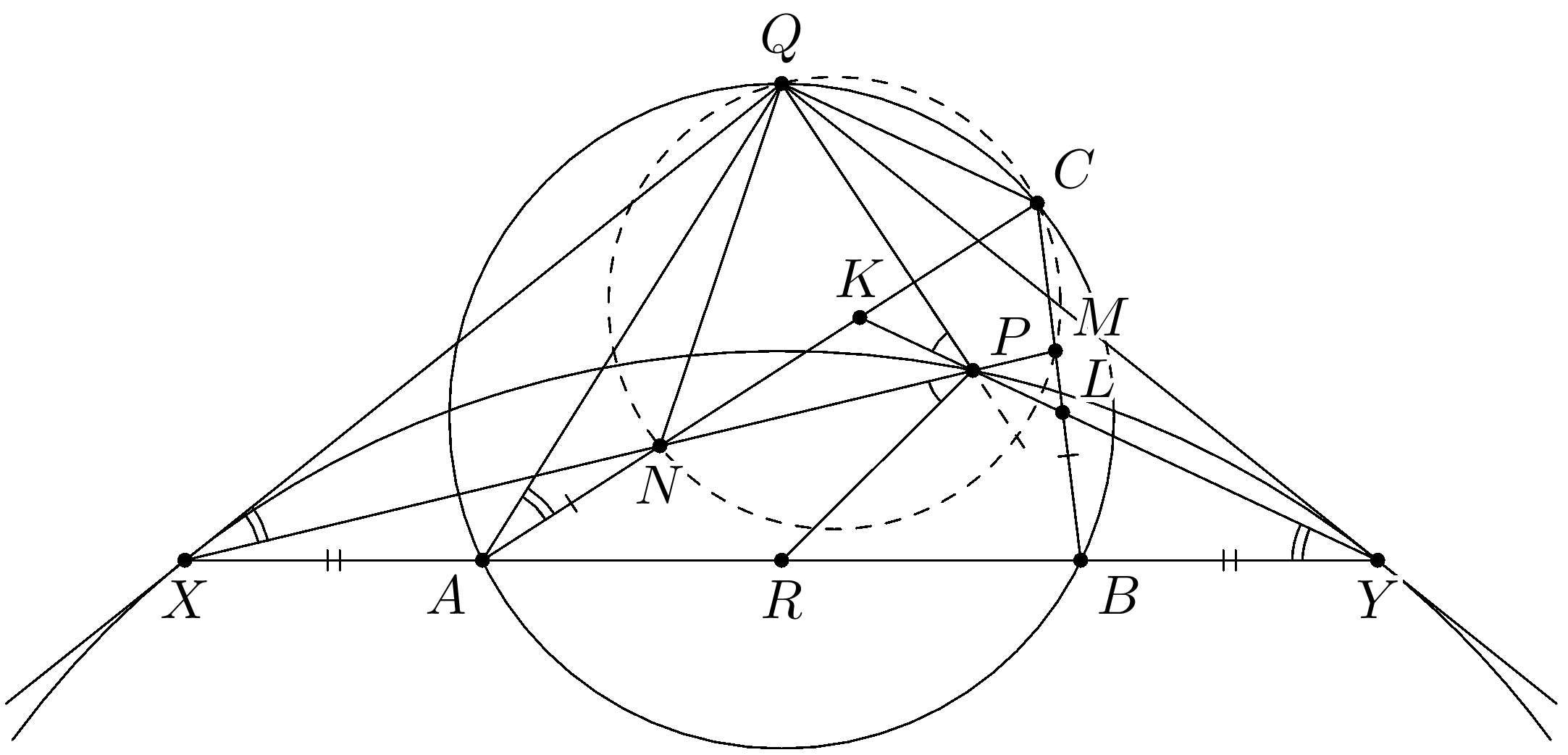
Так как $QA = QB$, $AN = BM$ и $\angle CAQ = \angle CBQ$. Значит, треугольники $QAN$ и $QBM$ равны. Отсюда, в частности, следует, что $QM = QN$ и $\angle MQN = \angle ACB$. Из последнего равенства углов следует, что четырёхугольник $MQCN$ вписан в некоторую окружность. Тогда, из выписанности четырехугольников следует, что $\angle QCM = \angle QNX$, с другой стороны $\angle QCM = \angle QAX$, то есть $ \angle QNX= \angle QAX$ или четырехугольник $ANQX$ вписанный.
Далее, так как $Q$ середина дуги $ACB$, то $\angle QAC=\angle QAB-\angle CAB=(\angle A + \angle B)/2-\angle A=\frac{\angle B-\angle A}{2}$. Треугольник $CKL$ равнобедренный, поэтому $\angle KYX = \angle CBA - \angle BLY= \angle B-(90^\circ - \angle C/2)=\angle B-(\angle A/2+\angle B/2)=(\angle B-\angle A)/2$, то есть $$\angle QXN=\angle QAN=(\angle B-\angle A)/2=\angle PYX.$$ Так как треугольник $QXY$ равнобедренный, то $\angle PXY =\angle PYQ$.
Следовательно, прямые $QX$ и $QY$ — касательные к описанной окружности треугольника $PXY$. Тогда по свойству симедианы, прямая $QP$ как раз и есть симедиана треугольника $PXY$. Значит, $\angle QPK =\angle XPR = \angle RPN$.