1-я международная Иранская олимпиада по геометрии, 2014 год, вторая лига

Дан прямоугольный треугольник с углами $\angle A=90^\circ$ и $\angle C=30^\circ$. Обозначим через $\Gamma$ окружность, проходящую через точку $A$ и касающуюся отрезка $BC$ в его середине. Пусть $\Gamma$ пересекает отрезок $AC$ в точке $N$, а описанную окружность $\triangle ABC$ во второй раз точке $M$. Докажите, что $MN \perp BC$.

Комментарий/решение

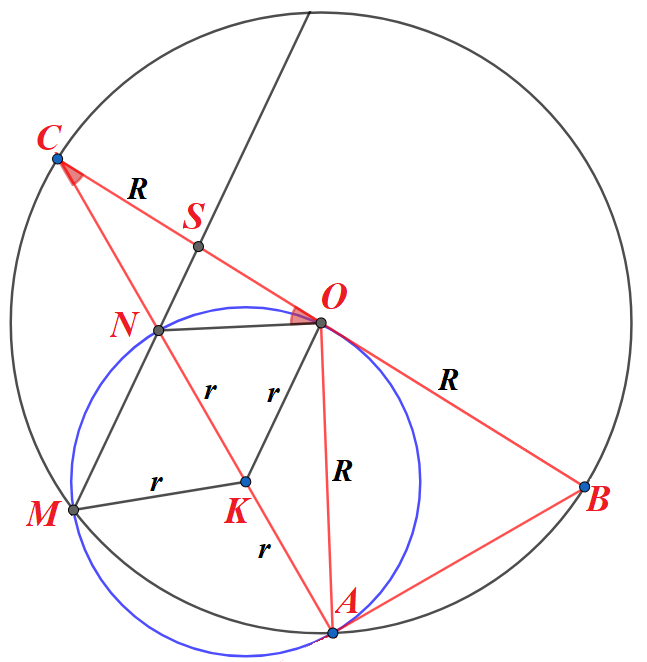
$$\triangle AOC: AO=OC=R\Rightarrow \angle OCA=\angle OAC=30^o$$

$$\angle OAC=\angle OAN=30^o\Rightarrow \angle NOC =30^o$$

$$ \angle NOC +\angle NOK=90^o\Rightarrow \angle NOK=60^o$$

$$ OK=NK=MK \Rightarrow \angle ONK = \angle MNK =60^o\Rightarrow \angle SNO=60^o$$

$$\angle SNO+\angle SON=90^o \Rightarrow \angle OSN=90^o \Rightarrow MN \bot BC$$

Так как $Γ$ касается $BC$, то середина $ΑΝ$ центр $Γ$. Симметрия относительно серпера к $BC$ дает что $A$ и $M$ симметричны, значит $AB=CM$, то есть $AM\parallel BC$. $AN$ диаметр $Γ$, значит $AM\bot MN$, то есть $BC\bot MN$

Обозначим через $K$ середину $BC$, проведем $MK$, $AK$ $= \frac{BC}{2}$, обозначим $\angle{MNA} = \alpha$, $\angle{MKA} = \alpha$, $\bigtriangleup AKD$ - равносторонний, $\angle{KAB} = 60$, так как K середина окружности описанной около треугольника ABC, $\Rightarrow MK=AK, AMK$ равносторонний $\Rightarrow \alpha = 60, MN \bot BC$