Районная олимпиада, 2001-2002 учебный год, 9 класс


В трапецию можно вписать окружность. Доказать, что окружности, построенные на её боковых сторонах, как на диаметрах касаются друг друга.
посмотреть в олимпиаде

Комментарий/решение:

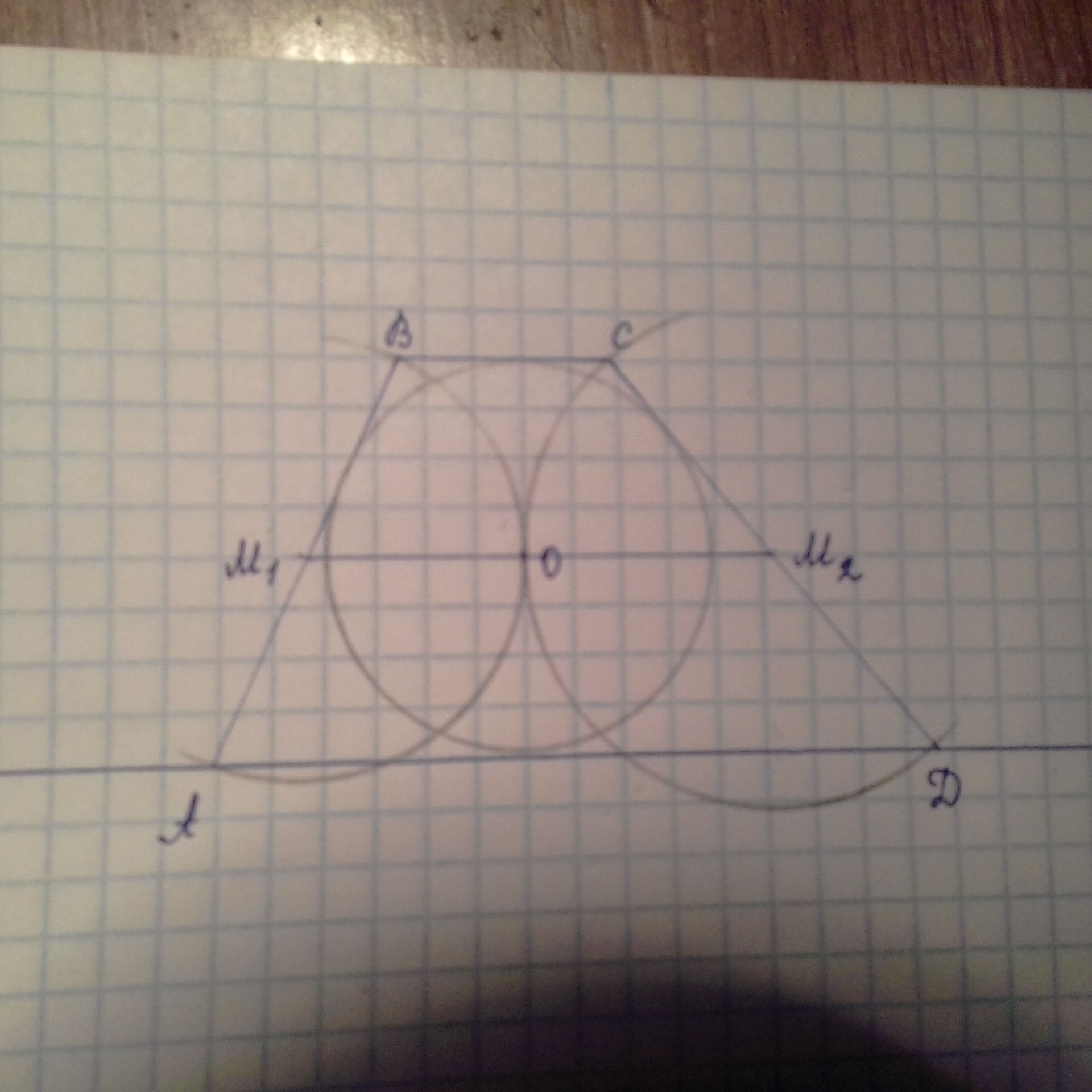
пред. Правка 2   3 | проверено модератором
2017-07-06 04:46:10.0 #

По условию в трапецию $ABCD $ вписана окружность. Из этого следует, что $AB+CD=BC+AD $.Пусть $M_1, M_2$-середины отрезков $AB $и $CD $ соответственно. Значит, $M_1M_2$-средняя линия по построению

$$R_1+R_2=M_1B+M_2C=\dfrac {AB}{2}+\dfrac {CD }{2}=\dfrac {BC+AD}{2}=M_1M_2.$$

То есть, расстояние от центров окружности равно сумме радиусов. А это и есть условие касание окружностей.

1234567