Республиканская олимпиада по математике, 2018 год, 10 класс
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1.
Решение. Пусть прямые $CL$ и $BM$ пересекаются в точке $P$, а прямые $PK$ и $AD$ — в точке $Q$. Достаточно доказать, что $PQ$ — биссектриса угла $AKD$ или $AQ/AK=DQ/DK$.
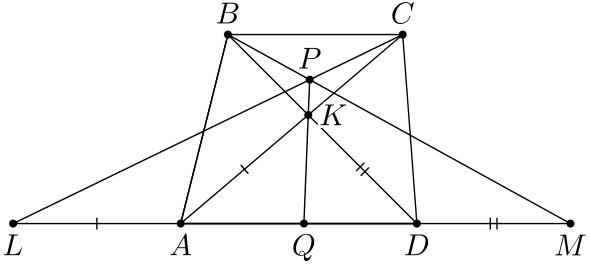
Пусть $ X \in BM \cap CL$ если биссектриса $\angle BKC$ проходит через $X$, то воспользуемся теоремой Чевы для треугольника $BKC$ в угловой форме, получим
$$\dfrac{\sin \angle DBM}{\sin \angle MBC} \cdot \dfrac{ \sin \angle BCL}{\sin \angle ACL} = 1 $$ докажем это.
Так как $\angle CBM = \angle DMB$ и $\angle BCL = \angle ALC$ откуда
$\dfrac{\sin \angle DBM}{\sin \angle CBM} = \dfrac{\sin \angle DBM}{\sin \angle DMB} = \dfrac{DM}{BD} = \dfrac{DK}{BD}$ аналогично и с другим , получаем $\dfrac{DK}{BD} = \dfrac{AK}{AC}$ или $\dfrac{BK}{CK} = \dfrac{KD}{AK}$
что следует из подобия треугольников $BKC,AKD$.

Пусть пересечение $BM, CL$ будет $P$. Необходимо доказать, что перпендикуляры $PQ$ и $PR$ на $AC$ и $BD$, соответственно, равны. Пусть $LS$,$MT$ и $KH$ - перпендикуляры на прямые $AC$,$BD$ и $AD$, соответственно. Тогда очевидно, что $\triangle LAS=\triangle KAH$, откуда $LS=KH$. Аналогично $MT=KH=LS$. Из $\triangle BPC\sim\triangle MPA$ получаем, что $\frac{CP}{PA}=\frac{BP}{PA}\Rightarrow\frac{CP}{CA}=\frac{BP}{BM}=k$. Так как $\triangle BPR\sim\triangle BMT$, получаем $PR=MT\cdot k$, аналогично $PQ=LS\cdot k=MT\cdot k=PR$. Что требовалось доказать

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.