Районная олимпиада, 2000-2001 учебный год, 10 класс
Комментарий/решение:
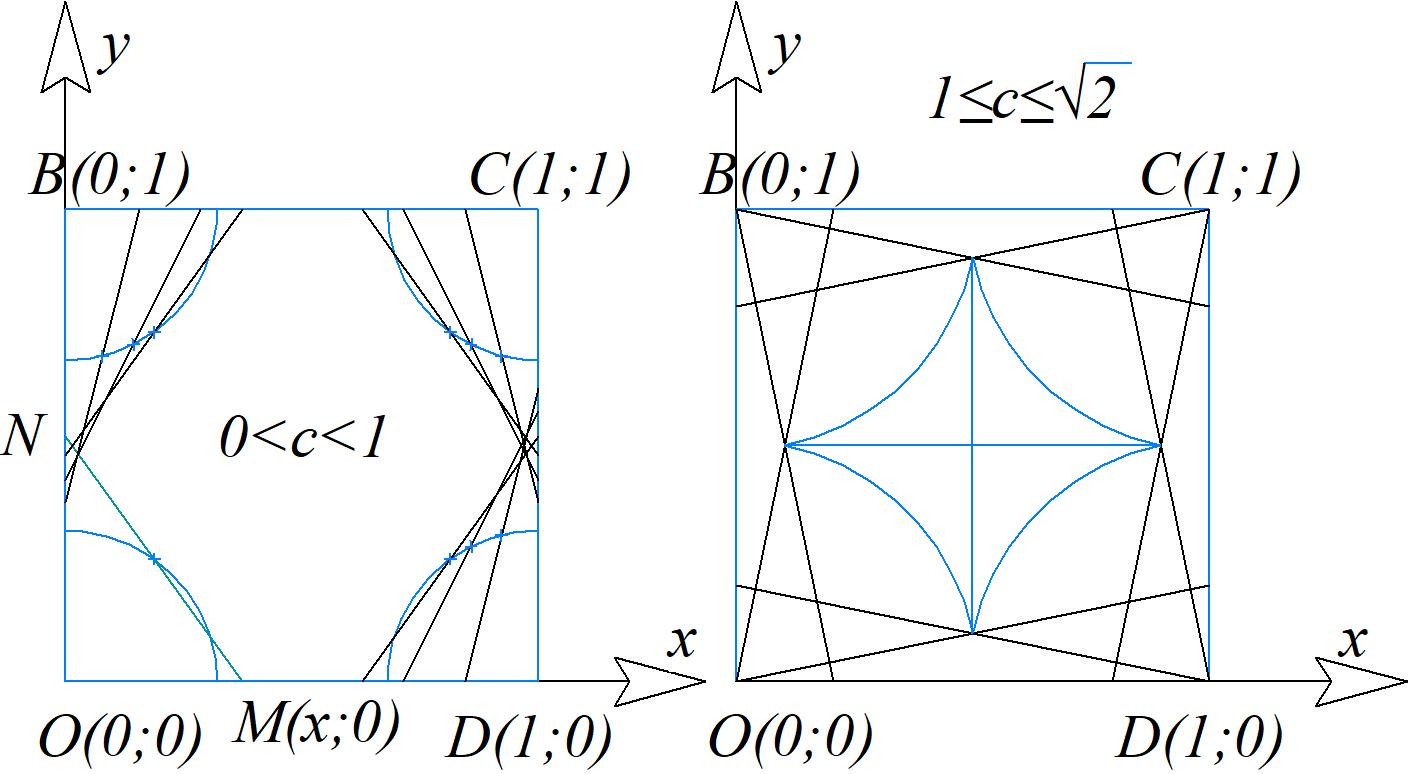
1)Рассмотрим прямоугольную декартову систему координат (ПДСК) с центром в точке $O(0;0)$
2)Построим в первом квадранте квадрат $OBCD$ со стороной $1$. Координаты вершин: $O(0;0);B(0;1);C(1;1);D(1;0)$
3)Вообще, смысл имеют значения $0<c\le\sqrt 2$. При $c=\sqrt 2$ возможно всего 2 положения отрезка длины $c$- по диагоналям квадрата, откуда в этом частном случае ГМТ точек – точка $(0.5;0.5)$. При $c>\sqrt 2$ отрезок не сможет лежать сразу на двух сторонах внутри квадрата.
4)Рассмотрим случай $0<c\le 1$. Поставим на стороне $OD$ произвольную точку $M(x;0)$
Пусть отрезок $MN$ имеет длину $|MN|=c$. Тогда координата точки $N$ вычислим с помощью теоремы Пифагора
$$ON^2+OM^2=c^2\Rightarrow Y_N=\sqrt {c^2- OM^2}=\sqrt {c^2- x^2}$$
5)Пусть середина отрезка $MN-$ точка $F$, тогда ее координаты
$$F\left(\dfrac{X_M+X_N}{2};\dfrac{Y_M+Y_N}{2}\right) =\left(\dfrac{x}{2};\dfrac{\sqrt {c^2- x^2}}{2}\right)$$
6)Но ведь утверждение (5) буквально описывает некоторую окружность. Проверим это.
$$X_F^2+Y_F^2=R^2$$
$$\dfrac{x^2}{4}+\dfrac{c^2-x^2}{4}\equiv \dfrac{c^2}{4}\forall x\Rightarrow R=c/2$$
Циклической перестановкой вершин (например $O\rightarrow B;B\rightarrow C;C\rightarrow D;D\rightarrow O$) можно показать аналогичные уравнения кривой для каждой вершины. То есть, если $0<c\le 1$, то искомое ГМТ- это четверть окружности радиусом $c/2$, лежащая внутри квадрата, с центром в каждой из вершин.
7)Теперь рассмотрим $1<c<\sqrt 2$. В данной ситуации отличие будет заключаться в том, что концы отрезка $MN$ будут лежать на противоположных сторонах квадрата, а не на сторонах, составляющих угол $90^\circ$. Поставим на стороне $OD$ произвольную точку $M(x;0)$.У точки $N$ игрековая компонента уже известна - это $Y_N=1$. По теореме Пифагора найдем $X_N$
$$(X_N-X_M)^2+(Y_N-Y_M)^2=c^2\Rightarrow (X_N-x)^2+(1-0)^2=c^2$$
$$X_N=x\pm \sqrt{c^2-1^2}$$
8)Как и в (5), отыщем середину получившегося отрезка
$$F\left(\dfrac{X_M+X_N}{2};\dfrac{Y_M+Y_N}{2}\right) =\left(\dfrac{2\cdot x\pm \sqrt{c^2-1}}{2};\dfrac{1}{2}\right)$$
Получается, что точки $F$ лежат по прямой, на высоте $Y_F=1/2$. Остается выяснить крайние координаты полученного ГМТ (отрезка)
9) А для этого рассмотрим два крайних случая: $N=B$ и $N=C$
$$if \;\;N=B:\;x=\sqrt{c^2-a^2}\Rightarrow x_{\min}=\dfrac{2\sqrt{c^2-1}-\sqrt{c^2-1}}{2} =\dfrac{\sqrt{c^2-1}}{2} $$
$$if \;\;N=C:\;x=1\Rightarrow x_{\max}=\dfrac{2\cdot 1-\sqrt{c^2-1}}{2} $$
10)Циклической перестановкой вершин (например $O\rightarrow B;B\rightarrow C;C\rightarrow D;D\rightarrow O$) можно показать аналогичные уравнения кривой для каждой стороны. То есть, если $1<c<\sqrt 2$, то искомое ГМТ- это два взаимно перпендикулярных отрезка длиной $L=1-\sqrt{c^2-1}$ каждый, причем пересекаются эти отрезки посередине друг друга, а точка пересечения совпадает с точкой пересечения диагоналей + четвертинки окружности из случая $0<c<1$.
11) Асимптотическая проверка: при длине отрезка $|MN|=\sqrt 2$
$$L=1-\sqrt{(\sqrt 2)^2-1}=0$$
То есть, как и ожидалось, отрезки выродились в точку
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.