Областная олимпиада по математике, 2019 год, 9 класс

Окружность с центром в точке $I$, вписанная в неравнобедренный треугольник $ABC$, касается сторон $AB,$ $BC$ и $AC$ в точках $D,$ $E$ и $F$ соответственно. Прямые $AI$ и $BI$ пересекают прямую $EF$ в точках $M$ и $N$ соответственно. Пусть $G$ — середина отрезка $AB.$ Докажите, что точки $M,$ $N,$ $D$ и $G$ лежат на одной окружности.

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.    
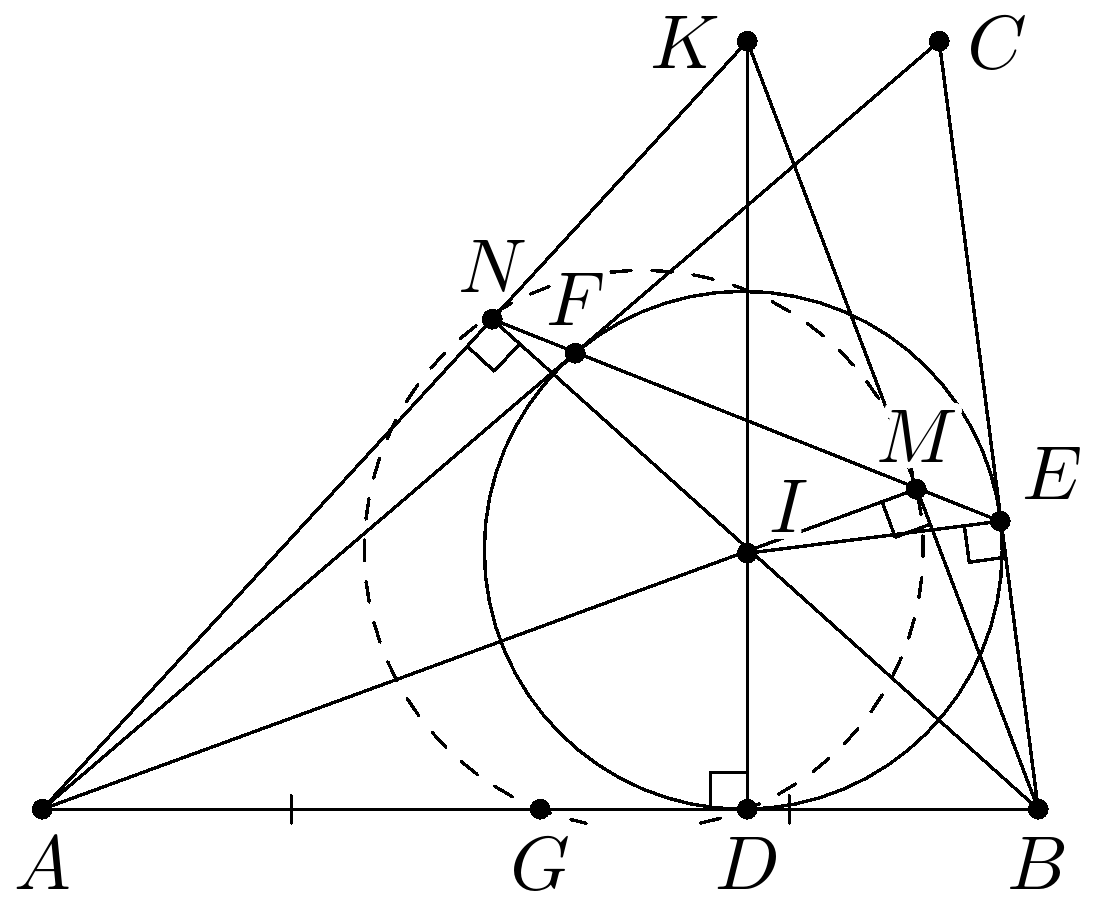
Решение. Докажем, что $\angle AMB=90^\circ$ (см. рис. ниже). Точки $I$, $M$, $E$ и $B$ лежат на одной окружности, так как если $M$ лежит на отрезке $EF$, то $$\angle BIM = \frac{\angle A}{2}+ \frac{\angle B}{2} = 90^\circ -\frac{ \angle C}{2} = \angle CEM =180^\circ - \angle MEB;$$ если же точка $M$ — на продолжении $EF$, то $\angle BIM = \angle BEM$. Таким образом, $\angle AMB=\angle IMB = \angle IEB = 90^\circ$. Аналогично, $\angle ANB=90^\circ$. Пусть $AN$ и $BM$ пересекаются в точке $K$. Тогда $I$ — ортоцентр $\triangle AKB$. Так как $ID \perp AB$, то $K$ лежит на прямой $ID$. Осталось заметить, что точки $M,$ $N,$ $D$ и $G$ лежат на окружности девяти точек треугольника $ABK$.