Областная олимпиада по математике, 2019 год, 11 класс
В треугольнике $ABC$ проведена биссектриса $AD$, а биссектриса внешнего угла при вершине $A$ во второй пересекает описанную окружность треугольника $ABC$ в точке $P.$ Некоторая окружность, проходящая через точки $A$ и $P$, во второй раз пересекает отрезки $BP$ и $CP$ в точках $E$ и $F$ соответственно. Докажите, что $\angle DEP=\angle DFP.$
посмотреть в олимпиаде
Комментарий/решение:
Комментарии от администратора Комментарии от администратора №1.
Решение. Пусть $AB \ge AC$. Для решения задачи достаточно показать подобие $\triangle DEB \sim \triangle DFC$ (см. рис. ниже).
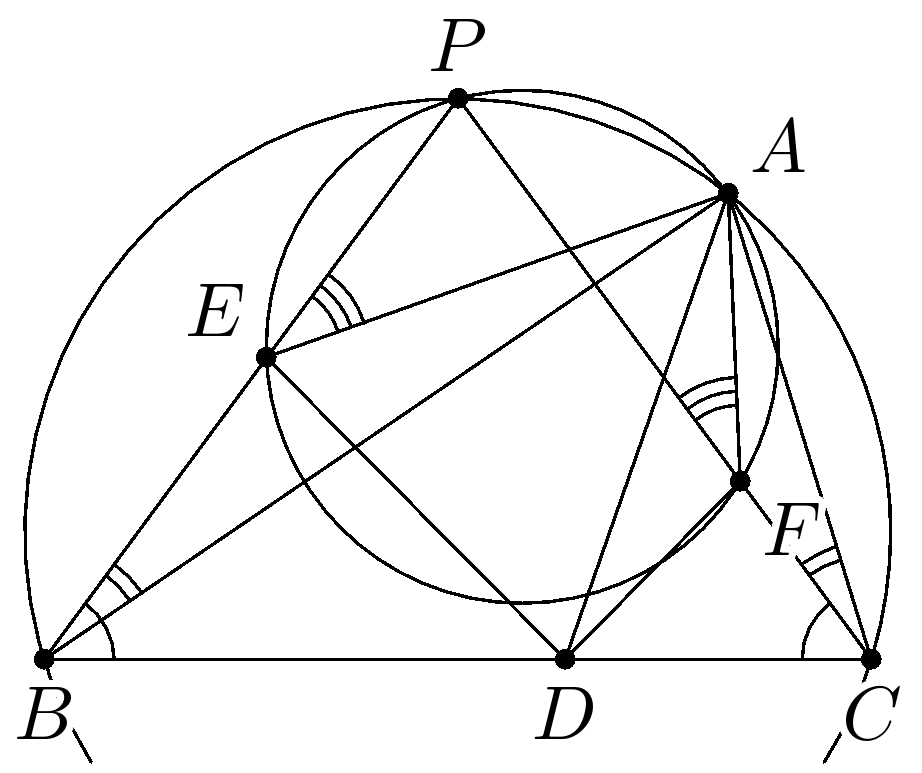
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.