Областная олимпиада по математике, 2019 год, 11 класс


Каждая точка плоскости окрашена в один из четырех цветов. Докажите, что найдутся две точки $A$ и $B$ одного цвета такие, что $AB=1$ или $AB=\sqrt{3}$.
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.    
Решение. Решим задачу от противного. Полагая, что не найдутся две точки $A$ и $B$, удовлетворяющие условию задачи, сформулируем и докажем две леммы.
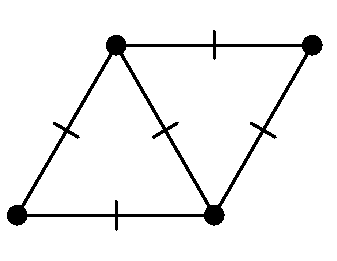
Лемма 1. Все четыре вершины ромба со стороной 1 и острым углом $60^\circ$ покрашены в разные цвета.
Доказательство . Легко посчитать, что диагонали такого ромба равны 1 и $\sqrt{3}$, следовательно по предположению четыре вершины ромба имеют разный цвет.


Лемма 2. Любые две точки на расстоянии 2 покрашены в одинаковый цвет.
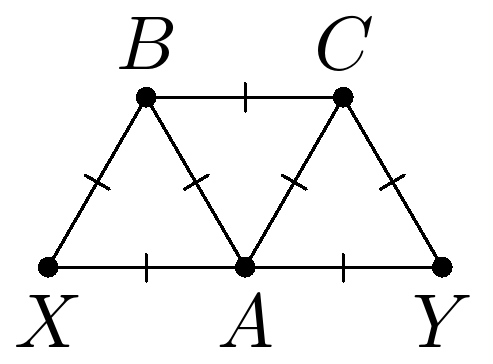
Доказательство . Рассмотрим произвольные точки $X$ и $Y$ такие, что $XY=2$. Отметим точки $A,$ $B,$ $C$ так, что $AXB,$ $ABC,$ $ACY $ равносторонние треугольники со стороной 1. По лемме 1 точки $A,$ $X,$ $B,$ $C$ покрашены в разные цвета. Также по лемме 1 точки $A,$ $B,$ $C,$ $Y$ покрашены в разные цвета. Следовательно точки $X$ и $Y$ одного цвета.


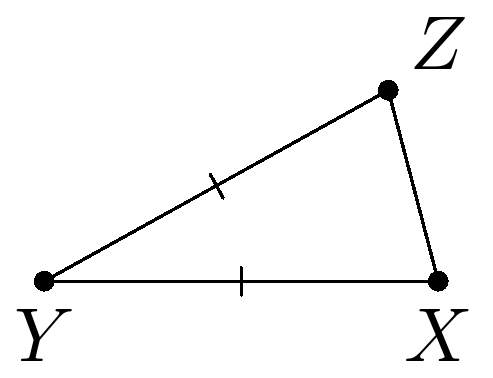
   Вернемся к решению. Рассмотрим треугольник $XYZ,$ где $XY=YZ=2$ и $XZ=1.$ По лемме 2 точки $X$ и $Y$ одного цвета. Также по лемме 2 точки $Y$ и $Z$ одного цвета. Следовательно точки $X$ и $Z$ одного цвета и $XZ=1,$ противоречие.