Республиканская олимпиада по математике, 2019 год, 9 класс

В прямоугольном треугольнике $ABC$ точка $D$ симметрична точке $C$ относительно гипотенузы $AB$. Пусть $M$ — произвольная точка отрезка $AC$, а $P$ — основание перпендикуляра из точки $C$ на прямую $BM$. Точка $H$ — середина отрезка $CD$. На отрезке $CH$ (внутри угла $HPB$) нашлась такая точка $N$ , что $\angle DPH = \angle NPB$. Докажите, что точки $M$, $P$, $N$ и $D$ лежат на одной окружности. ( М. Кунгожин )

Комментарий/решение

Легко понять, что точки $P$ и $H$ лежат на одной окружности с диаметром $BC.$ Также заметим, что $BP\cdot BM=BC^2=BD^2,$ то есть описанная окружность треугольника $MPD$ касается прямой BD. Тогда $\angle PMD=\angle PDB.$ Так как $\angle NDB=\angle BCH=\angle BPH=\angle DPN,$ то $\angle PMD=\angle PDB=\angle PDN+\angle NDB=\angle PDN + \angle DPN= \angle PNC$ или $\angle PMD=\angle PNC.$ Получилось, что в четырехугольнике $MPND$ внутренний угол при вершине $M$ равен внешнему углу при вершине $N,$ то есть он вписанный.

Из условия (пользуясь Теоремой Евклида) получаем, что $BD^2=BC^2=BP\cdot BM,$ откуда окружность $(MPD)$ касается прямой $BD$ в точке $D.$

Заметим, что $HPCB$ вписанный четырехугольник с диаметром $BC,$ следовательно $\angle BPH=\angle BCH=\angle BDN.$

Из равенства $\angle DPH=\angle NPB,$ получаем $\angle BPH=\angle NPD.$ Значит $\angle DPN=\angle NDB,$ то есть окружность $(NPD)$ касается прямой $BD$ в точке $D.$

По итогу окружности $(MPD)$ и $(NPD)$ совпадают, откуда следует требуемое. $\quad\blacksquare$

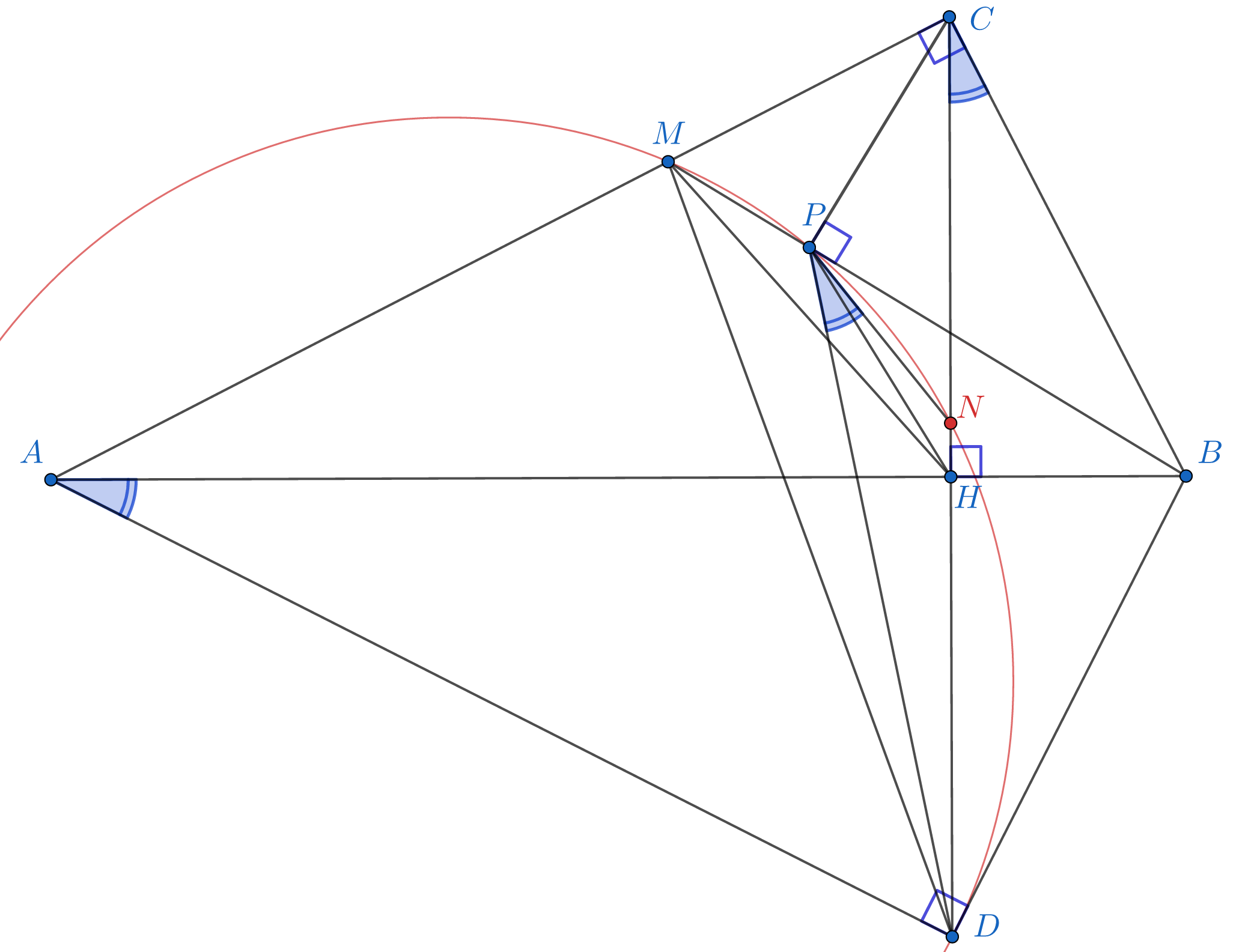
Решение можете посмотреть на данном сайте в разделе математика:

Республика 2019