XVIII математическая олимпиада «Шелковый путь», 2019 год


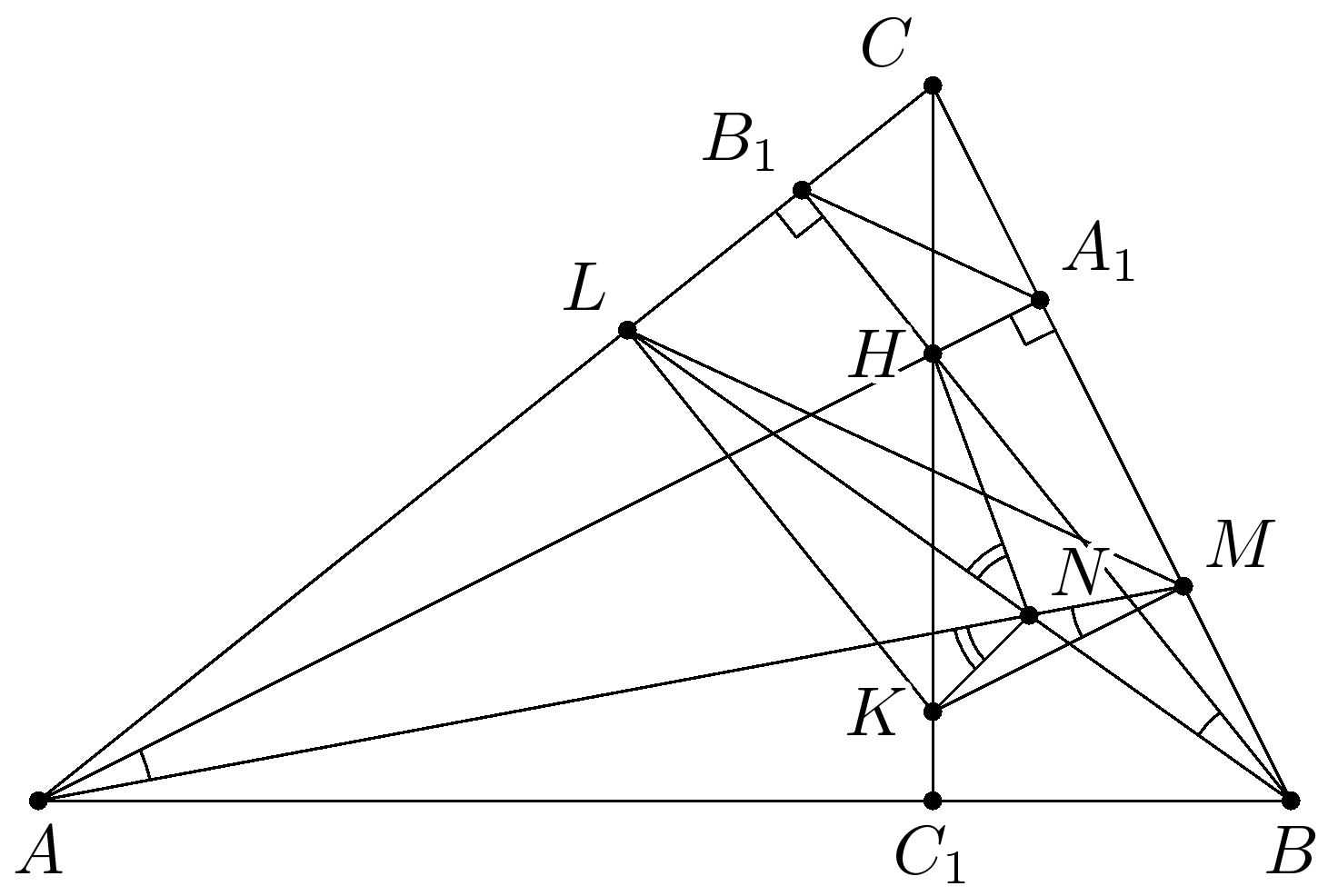
Высоты остроугольного неравнобедренного треугольника $ABC$ пересекаются в точке $H$. На отрезке $C_1H$, где $CC_1$ — высота треугольника, отмечена точка $K$. Точки $L$ и $M$ — основания перпендикуляров из точки $K$ на прямые $AC$ и $BC$ соответственно. Прямые $AM$ и $BL$ пересекаются в точке $N$. Докажите, что $\angle ANK=\angle HNL$. ( М. Кунгожин )
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.     Пусть $AC > BC$ и $AA_1$, $BB_1$ — высоты треугольника $ABC$. Так как $\frac{CB_1}{B_1L}=\frac{CH}{HK}=\frac{CA_1}{A_1M}$, то $A_1B_1 \parallel ML$. Четырехугольник $AB_1A_1B$ вписан в окружность с диаметром $AB$. Поэтому из вписанности и параллельности следует $\angle LMC=\angle B_1A_1C=\angle CAB$, то есть и четырехугольник $ALMB$ вписанный. Вписанность этих четырехугольников даёт следующее равенство: $ \angle MAH=\angle MAL-\angle A_1AC=\angle MBL-\angle MBB_1=\angle LBH$. Следовательно, $$\angle NMK=\angle MAH=\angle NBH. \quad (1)$$

Очевидно, что $\triangle ANB \sim \triangle LNM$ и $\triangle ABH \sim \triangle LMK$, так как $\angle ABH=\angle ACH=\angle LMK$ и $\angle BAH=\angle BCH=\angle MLK$. Следовательно, $$\frac{KM}{HB}=\frac{LM}{AB}=\frac{MN}{BN}. \quad (2)$$ Значит, $\triangle KMN \sim \triangle HBN$ (по двум сторонам и углу между ними). Тогда углы углы $ANK$ и $HNL$ равны, так как это внешние углы при соответствующих вершинах в подобных треугольниках.

  0
2024-12-03 11:53:01.0 #

Заметим что $(MLAB)$.

$\angle KMN=\angle KLB=\angle HBN$ так как $\angle BHK=\angle HKL$ и $HB||LK$

Отсюда следует что остается доказать $\frac{HB}{MK}=\frac{NB}{NM}=\frac{AB}{LM}$

$\frac{HB}{MK}=\frac{A_1B}{\sin C}*\frac{1}{CK*sin BCC_1}=\frac{AB}{CK*\sin C}=\frac{AB}{LM}$

IMO