Бат, Великобритания, 2019 год

В треугольнике $ABC$ точка $A_1$ лежит на отрезке $BC,$ а точка $B_1$ лежит на отрезке $AC.$ Пусть $P$ и $Q$ — точки на отрезках $AA_1$ и $BB_1$ соответственно, такие, что прямая $PQ$ параллельна $AB.$ Точка $P_1,$ лежащая на прямой $PB_1,$ такова, что $B_1$ находится строго между $P$ и $P_1,$ причем $\angle PP_1C=\angle BAC.$ Аналогично, точка $Q_1$, лежащая на прямой $QA_1,$ такова, что $A_1$ находится строго между $Q$ и $Q_1,$ причем $\angle CQ_1Q=\angle CBA.$ Докажите, что точки $P,$ $Q,$ $P_1$ и $Q_1$ лежат на одной окружности.

Комментарий/решение

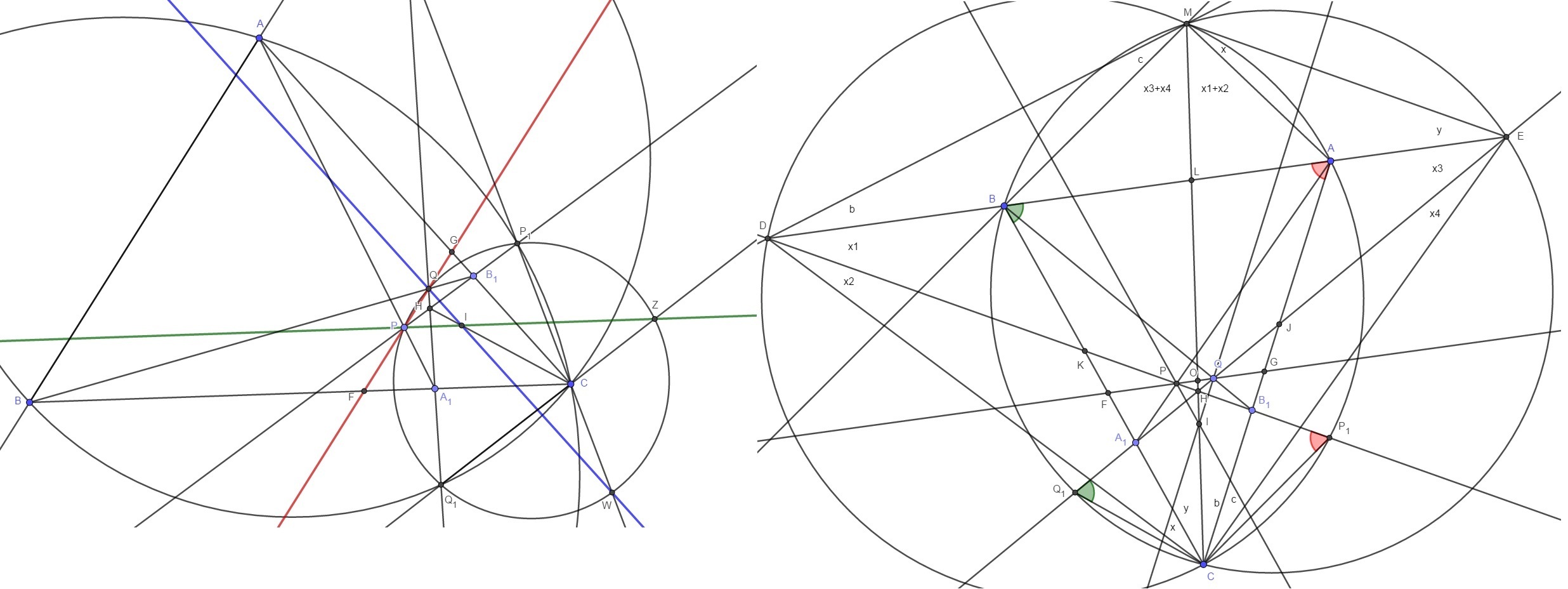
Определим точку $P_{1}$ для этого продлим до пересечения с $AB$ прямую $PB_{1}$ пусть это точка $D$ , опишем окружность $\omega_{1}$ около треугольника $DAC$ тогда $P_{1} \in \omega \cap PB_{1}$ аналогично определяется точка $Q_{1}$ с окружностью $\omega_{2}$ описанной около $BCE$.

Пусть $ K \in PB_{1} \cap BC, \ J \in QA_{1} \in AC, \ F \in PQ \cap BC , \ G \in PQ \cap AC$ пусть $ M \in \omega_{1} \cap \omega_{2}$ и $O \in CM \cap FG, \ L \in CM \cap AB$ .

Лемма: $DB_{1} , \ EA_{1}, \ CM$ пересекаются в одной точке $H \in CM$.

Доказательство:

1) докажем с начало что $KJ || AB$, для этого по теореме Фалеса докажем что

$\dfrac{KF}{BK} = \dfrac{GJ}{AJ}$ из параллельности $PQ || AB$ получается

$\dfrac{KF}{BK} = \dfrac{FP}{BD}$ из подобия $DBB_{1}, \ PQB_{1}$ получается $BD = \dfrac{BB_{1} \cdot PQ}{QB_{1}}$ подставляя $\dfrac{KF}{BK} = \dfrac{FP \cdot QB_{1}}{BB_{1} \cdot PQ}$ из подобия $BAA_{1}, \ FPA_{1}$ получается $FP =\dfrac{AB \cdot PA_{1}}{AA_{1}}$ подставляя $\dfrac{KF}{BK} = \dfrac{AB \cdot PA_{1} \cdot QB_{1}}{AA_{1} \cdot BB_{1} \cdot PQ}$ аналогично $\dfrac{GJ}{AJ} = \dfrac{QB_{1} \cdot AB \cdot A_{1}P}{AA_{1} \cdot PQ \cdot BB_{1}}$ то есть $KJ ||AB$.

2) Пусть $DB_{1}, EA_{1}$ пересекаются в точке $H \in CM$

По теореме Менелая для треугольника $DCL$ и секущей $DB_{1}$ и $ECL$ и секущей $\dfrac{LH}{CH} \cdot \dfrac{CK}{BK} \cdot \dfrac{DB}{DL} = \dfrac{LH}{CH} \cdot \dfrac{CJ}{AJ} \cdot \dfrac{AE}{EL}$ из доказанного выше $\dfrac{CK}{BK} = \dfrac{CJ}{AJ}$ откуда требуется доказать что $\dfrac{EL}{AE} = \dfrac{DL}{DB}$ или $\dfrac{AL}{AE} = \dfrac{BL}{BD} (1)$ (по положения углов как на картинке) $(1)$ можно записать как $ DB = \dfrac{BC \cdot sinx}{sin(x_{1}+x_{2})}, \ AL = \dfrac{AC \cdot sinb}{sinL} , \ BL =\dfrac{AB \cdot siny}{sinL} , \ AE=\dfrac{AC \cdot sinc}{sin(x_{3}+x_{4})}$ подставляя $(1)$ получается $ \dfrac{sinx}{siny} \cdot \dfrac{sinb}{sin(x_{1}+x_{2})} \cdot \dfrac{sin(x_{3}+x_{4})}{sinc} = 1$ которая есть теорема Чевы в угловой форме для треугольника $DCM$ для отрезков $DB, \ CB, \ MB$.

Лемма: Прямые параллельные $BC,AC$ и проходящие соответственно через $P,Q$ и $CM$ пересекаются в одной точке $I$.

Доказательство: Для доказательство требуется доказать что $\dfrac{OP}{FP} = \dfrac{OQ}{QG}$ для треугольника $COF$ и сеущей $KH$ и $COG$ и секущей $JH$ применяя теореме Менелая $\dfrac{CH}{OH} \cdot \dfrac{OP}{FP} \cdot \dfrac{KF}{KC} = \dfrac{CH}{OH} \cdot \dfrac{OQ}{QG} \cdot \dfrac{JG}{JC}$ учитывая параллельность $KJ || FG$ откуда и следует утверждение.

4) Докажем утверждение сказанное в условии. (2 способа)

1.

Пусть $Z \in PI \cap CQ_{1}$ и $W \in QI \cap P_{1}C$ так как $\angle PZI = \angle A_{1}CQ_{1} = \angle PQI = \angle BAC$ тогда $PQZQ_{1}$ вписанный

Тогда для вписанного четырехугольника $PQZQ_{1}$ точки $P_{1},W$ должны лежать так же на этой окружности , так как пары троек $Q, \ P_{1}, \ Z$ и $P, \ Q_{1}, \ W$ по теореме Паскаля лежат на одной прямой на которой лежат $H,I,C$ .

То есть $P,Q,P_{1},Q_{1}$ лежат на одной окружности.

2. По теореме Чевы в угловой форме для треугольников $PIQ$ и $IZW$

и учитывая вписанность $PQZQ_{1}, \ PQWP_{1}$ получается $\dfrac{\sin \angle HPI}{ \sin \angle IQH } = \dfrac{ \ sin \angle ZWC}{ \sin \angle CWQ} $ учитывая что $ \angle HPI + \angle IQH = \angle ZWC + \angle CWQ$ откуда $\angle HPI = \angle ZWC$ то есть $PQP_{1}Q_{1}$ лежат на одной окружности.

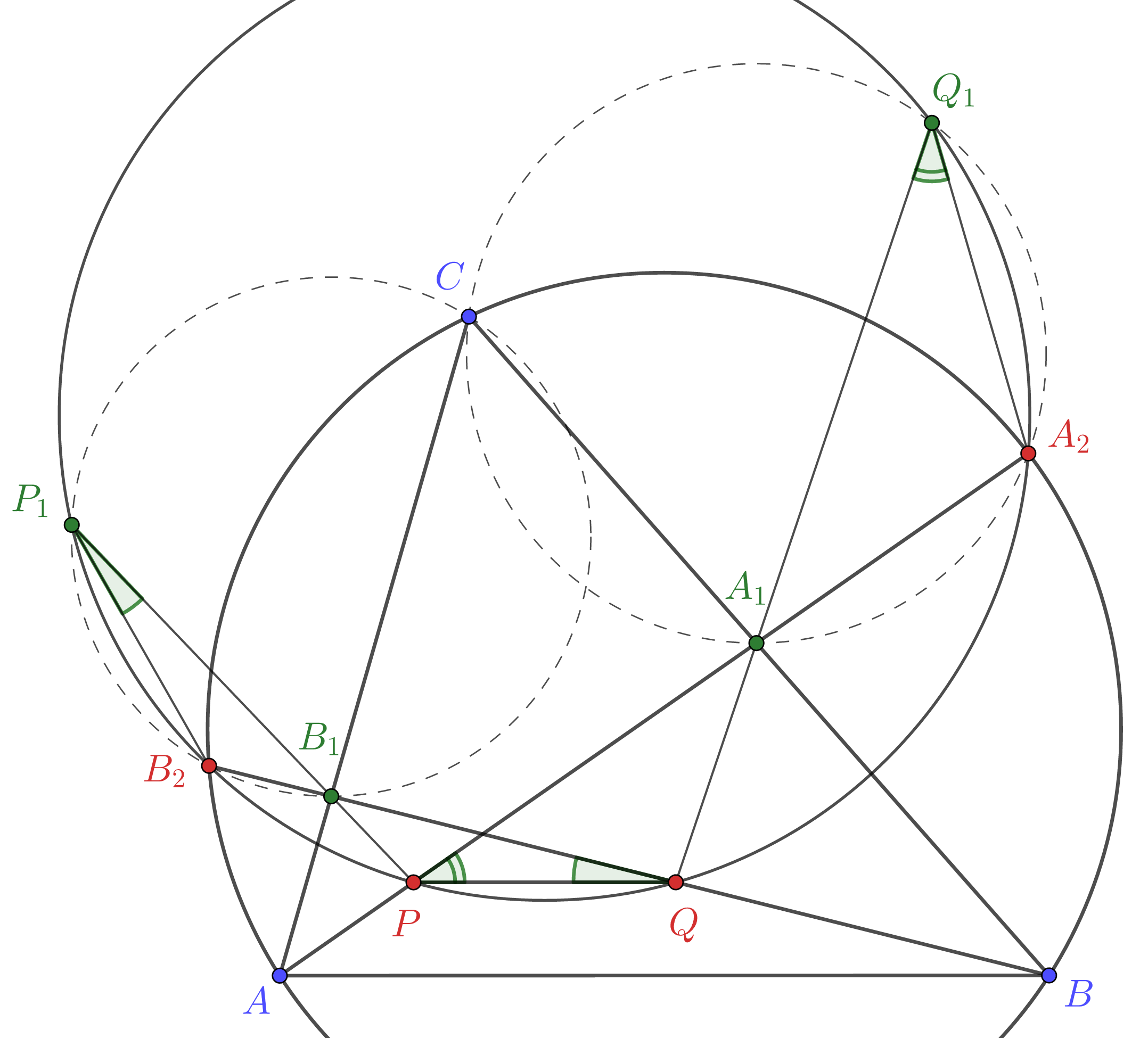
Решение: Через $(ABC)$ обозначим описанную окружность $\triangle ABC.$

Пусть $AA_1$ и $BB_1$ повторно пересекают $(ABC)$ в точках $A_2$ и $B_2,$ соответственно. Заметим, что $A_2B_2$ и $AB$ антипараллельны относительно $\angle (AA_2,BB_2),$ при этом $PQ\parallel AB\implies A_2B_2PQ$ $-$ вписанный.

Заметим, что $\angle CQ_1Q = \angle CBA = \angle CA_2A\implies CQ_1A_2A_1$ $-$ вписанный, откуда

$\angle A_2Q_1A_1 = \angle A_2CA_1 = \angle A_2AB = \angle A_2PQ,$ следовательно $Q_1\in (A_2B_2PQ),$ аналогично $P_1\in (A_2B_2PQ).$

Значит $P,Q,P_1,Q_1$ лежат на одной окружности.

$PB_1 \cap CB=A_2 , QA_1 \cap AC=B_2 , PQ \cap AC,BC=M,N$

\[ (P,Q;M,N) \overset{A_1}{=} (M,X;A,C) \]

\[ (P,Q;M,N) \overset{B_1}{=} (C,B;Y,N) \] отсюда из двойные отношение равны значит $\frac{XA}{XC}*\frac{MA}{MC}=\frac{YC}{YB}*\frac{NB}{NC}$ и тк $MN||AB => A_2B_2||AB$

$\angle ABC=\angle CB_2A_2=\angle CQ_1Q$ отсюда аналогично посчитав углы выходит что $P_1Q_1A_2B_2C$ вписанный. $\angle A_2P_1Q_1=\angle A_2CQ_1=\angle PQA_1$ отсюда $PQP_1Q_1$ вписаный .

вписанный