Геометриядан 6-шы Иран олимпиадасы, 2019 жыл, 2-ші лига, 9-10 сыныптар

Центрлері сәйкесінше $O_1$ және $O_2$ болатын $\omega_1$ және $\omega_2$ шеңберлері $A$ және $B$ нүктелерінде қиылысады, ал $O_1$ нүктесі $\omega_2$-де жатыр. $\omega_1$ шеңберінен кез келген $P$ нүктесі алынған. $BP$, $AP$ және $O_1O_2$ түзулері $\omega_2$-ны екінші рет сәйкесінше $X,$ $Y$ және $C$ нүктелерінде қияды. $XPYC$ төртбұрышының параллелограмм екенін дәлелдеңіз.

Комментарий/решение

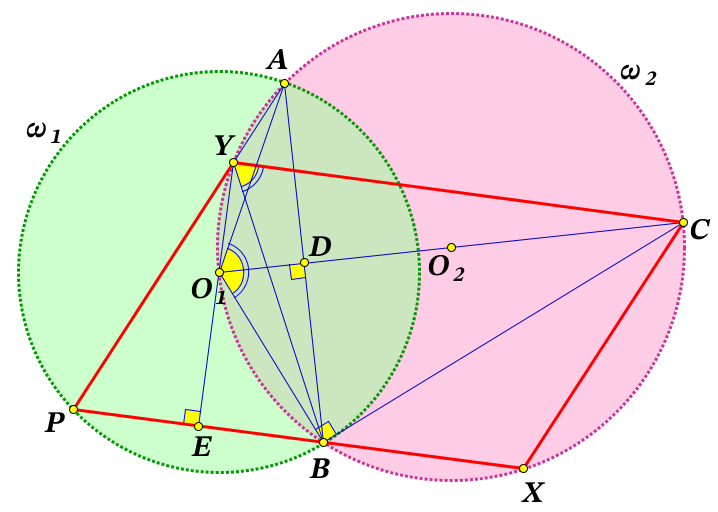
$$\textbf{Решение:} \quad \angle CXB=\alpha \Rightarrow \angle BYC=180^o-\alpha \Rightarrow \angle BYC=\angle BO_1C=180^o-\alpha$$

$$\angle APB=\frac{\angle AO_1B}{2}=\angle BO_1C=180^o-\alpha \Rightarrow \begin{cases} \angle CXB=\alpha \\ \angle APB=180^o-\alpha \end{cases}\Rightarrow AP\parallel XC$$

$$\angle CYO_1=90^o, \quad YO_1\bot PB \Rightarrow \angle PYE=90^o-\angle YPE=90^o-(180^o-\alpha)=\alpha-90^o$$

$$\angle PYC=\angle PYE+\angle CYE=\alpha-90^o+90^o=\alpha \Rightarrow \begin{cases} \angle PYC=\alpha \\ \angle YPX=180^o-\alpha \end{cases}\Rightarrow PX \parallel YC$$

Откуда YO_{1} перпендикулярна PB, можете объяснить пожалуйста?

Е-пересечение $YO_{1}$ и $PB$ то

$\angle{O_{1}BY}=\angle{O_{1}CY}=\angle{O_{1}AY}$ т.к. все точки лежат на одной окружности и смотрят на одну дугу

Заметим, что $O_{1}P=O_{1}A$ т.к. радиус. Тогда $\angle{O_{1}AY}=\angle{O_{1}PA}$ Так же известно, что $\angle{O_{1}BP}=\angle{O_{1}PB}$

$\angle{PBY}=\angle{BPY} \Rightarrow PY=PB$ известно, что серединный перпендикуляр $PB$ проходит через $O_1$ т.к. это центр описанной. Так же известно, что серединный перпендикуляр $PB$ проходит через $Y$ т.к. у равнобедренного треугольника и высота и медиана один отрезок. Значит $YO_{1}$ лежит на серединном перпендикуляре и $YE$ серединный перпендикуляр $BP$