XIV математическая олимпиада «Шелковый путь», 2020 год

Шексіз және қатаң өспелі $a_1,$ $a_2,$ $a_3,$ $\ldots$ натурал сандар тізбегі берілген. Барлық натурал $n$ саны үшін $a_n \leq n+2020$ екені және $n^3 a_n - 1$ саны $a_{n+1}$ санына бөлінетіні белгілі. Кез келген натурал $n$ үшін $a_n = n$ екенін дәлелдеңіз. ( М. Кунгожин )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Пусть $AC \leq BC$. Отметим на стороне $AB$ точку $D$ такую, что $DM \parallel BC$. Тогда \[\frac{DB}{DA} = \frac{CM}{AM} = \frac{BL}{CL},\] то есть $DL \parallel AC$. На касательной прямой к $\omega$ в точке $C$ отметим точку $T$ такую, что $KT \parallel BC$. Тогда $\angle TKA = \angle CBA = \angle TCA$. Следовательно, четырехугольник $AKCT$ — вписанный. Пусть отрезки $KT$ и $AC$ пересекаются в точке $S_1$. Тогда \[\frac{S_1P}{S_1C} = \frac{KP}{KL} = \frac{KA}{KD} = \frac{S_1A}{S_1M} \implies S_1P \cdot S_1M = S_1C \cdot S_1A = S_1K \cdot S_1T.\] Значит, четырехугольник $TMKP$ вписан в окружность, описанную около треугольника $KMP$. Известно, что общие хорды каждой пары трёх окружностей, центры которых не лежат на одной прямой, пересекаются в одной точке. Это значит, что общая хорда окружности $\omega$ и описанной окружности треугольника $KMP$ проходит через точку $S_1$. Следовательно, точки $S_1$ и $S$ совпадают, и параллельность $S_1K \parallel BC$ верна из построения точки $T$.

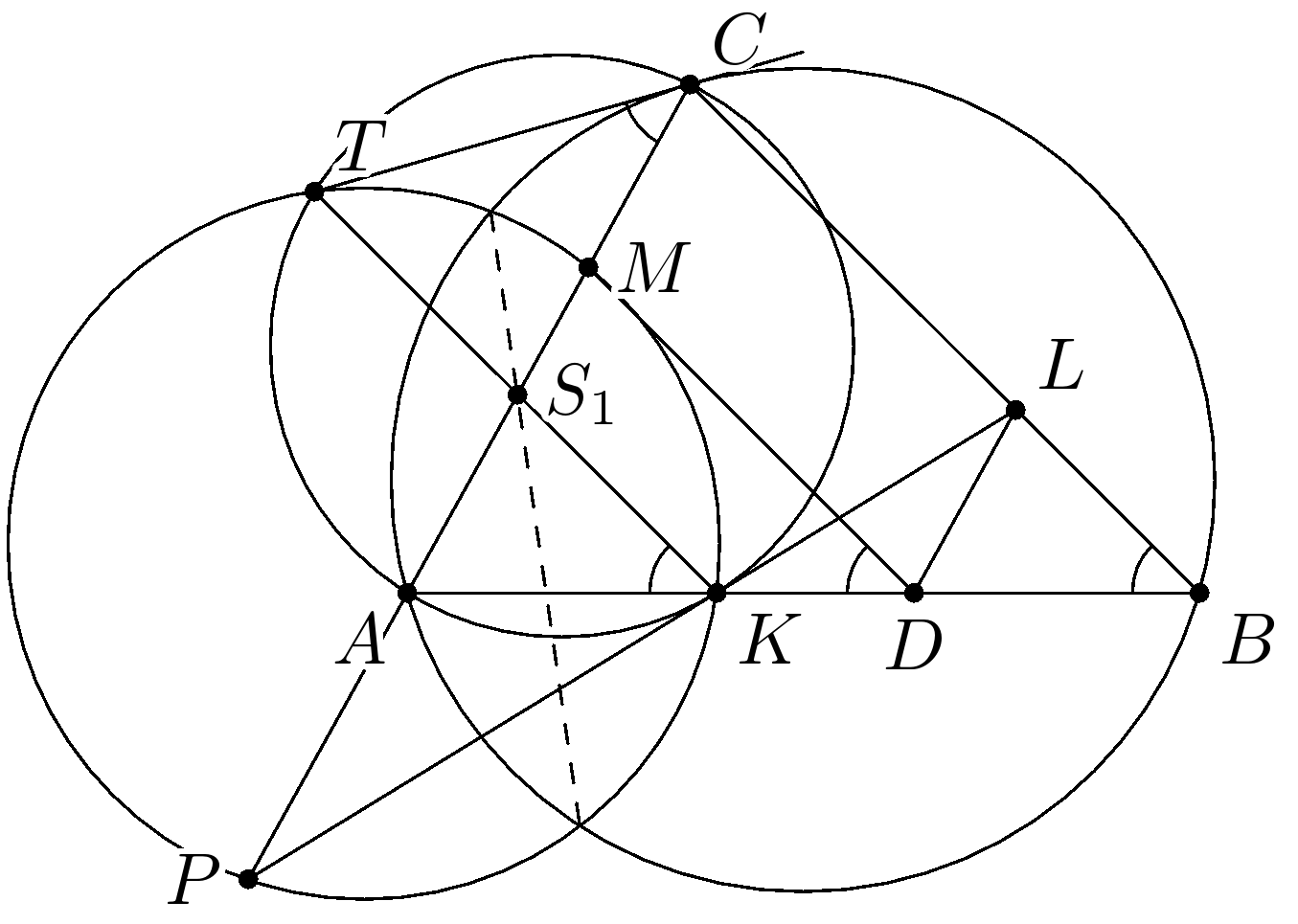
Комментарии от администратора Комментарии от администратора №2.     Введем обозначения: \[b = AC, \ m = AM, \ s = AS, \ p = AP.\] Так как $S$ лежит на радикальной оси описанных окружностей треугольников $ABC$ и $PKM$, то \[SM \cdot SP = SA \cdot SC \implies (m - s)(s + p) = s(b - s) \implies s = \frac{pm}{b + p - m}.\] Тогда \[\frac{AS}{SC} = \frac{s}{b - s} = \frac{pm}{(b - m)(b + p)}.\] По теореме Менелая для треугольника $ABC$ и секущей $PKL$: \[\frac{AK}{KB} \cdot \frac{BL}{LC} \cdot \frac{CP}{PA} = 1 \implies \frac{AK}{KB} = \frac{CL}{LB} \cdot \frac{AP}{PC} = \frac{AM}{MC} \cdot \frac{AP}{PC} = \frac{m}{b - m} \cdot \frac{p}{b + p} = \frac{AS}{SC} \implies SK \parallel BC,\] что и требовалось доказать.