XIV математическая олимпиада «Шелковый путь», 2020 год

Докажите, что для любого натурального числа $m$ существует такое натуральное $n$, что любые $n$ различных точек на плоскости можно разбить на $m$ непустых множеств, выпуклые оболочки которых будут иметь общую точку.
Выпуклой оболочкой конечного множества $X$ точек на плоскости называется множество точек, лежащих внутри или на границе хотя бы одного выпуклого многоугольника с вершинами в $X$, включая вырожденные, т. е. отрезок и точка считаются выпуклыми многоугольниками. Никакие три вершины выпуклого многоугольника не лежат на одной прямой. Многоугольник содержит свою границу. ( Зиманов А. )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Напомним теорему Хелли: если в конечном множестве выпуклых множеств точек на плоскости каждые три пересекаются, то и все пересекаются.
Докажем, что $n = 9m$ подходит. Пусть $X$ — произвольное множество из $9m$ различных точек на плоскости, а $Y$ — множество подмножеств $X$ размера $6m + 1$.
Предположим, что существуют такие $A, B, C \in Y$, что их пересечение пусто. Пронумеруем все точки из $X$ числами от 1 до $9m$. Выпишем на листе бумаги сначала все номера точек из множества $A$, затем из множества $B$ и в конце из множества $C$. В итоге, мы выпишем $|A| + |B| + |C| = 18m + 3$ числа. Так как эти три множества не пересекаются, то мы не могли выписать никакое число более, чем два раза. Значит, мы выписали не более $2 \cdot 9m = 18m$ чисел — противоречие. Следовательно, любые три элемента $Y$ пересекаются.
Так как выпуклая оболочка множества точек полностью содержит это множество, то выпуклые оболочки любых трех элементов $Y$ пересекаются. Следовательно, по теореме Хелли, выпуклые оболочки всех элементов $Y$ имеют какую-то общую точку $O$.
Докажем следующую лемму: если выпуклая оболочка какого-то конечного множества точек $Z$ содержит какую-то точку $P$, то существует $W \subseteq Z$, такое что $|W| \leq 3$ и выпуклая оболочка $W$ содержит $P$. По определению выпуклой оболочки, существует выпуклый многоугольник с множеством вершин $V \subseteq Z$ (возможно, вырожденный), который содержит эту точку $P$. Если $|V| \leq 3$, то $V$ подходит в качестве $W$. Иначе, сделаем произвольную триангуляцию многоугольника с вершинами в $V$. Точка $P$ должна лежать хотя бы в одном треугольнике разбиения. Множество вершин такого треугольника подходит в качестве $W$.
Заведем мешок, в который будем складировать непустые подмножества $X$. Определим следующую операцию, изменяющую $X$ и $Y$: выберем любое $A \in Y$. Так как выпуклая оболочка $A$ содержит $O$, то, по лемме, существует такое $B \subseteq A$, что $|B| \leq 3$ и выпуклая оболочка $B$ содержит $O$. Положим $B$ в мешок (очевидно, $B$ непусто), удалим элементы $B$ из $X$, и удалим из $Y$ множества, содержащие элементы $B$.
После одной операции мощность $X$ уменьшается не более, чем на три, и $Y$ непусто до тех пор, пока $|X| \geq 6m + 1$. Следовательно, мы можем выполнить операцию хотя бы $m$ раз. Выполним операцию ровно $m$ раз. Оставшиеся в $X$ точки распределим произвольным образом между множествами в мешке.
Итак, множества в мешке составляют разбиение начального множества точек на $m$ множеств и выпуклая оболочка каждого из них содержит точку $O$, т. е. они пересекаются, что нам и было нужно.

Комментарии от администратора Комментарии от администратора №2.     Индукцией по $m$ докажем, что любые хотя бы $4m^2$ различных точек на плоскости можно разбить на $m$ непустых множеств, выпуклые оболочки которых пересекаются. При $m = 1$ утверждение, очевидно, верно. Пусть оно верно для $m = k - 1$, где $k \geq 2$. Докажем, что оно верно и для $m = k$. Рассмотрим произвольное множество $X$ из хотя бы $4k^2$ различных точек на плоскости. Пусть $Y$ — подмножество точек $X$, лежащих на границе выпуклой оболочки всех точек из $X$. Если $|Y| < 4k$, то $|X \setminus Y| > 4k^2 - 4k > 4(k-1)^2$. По предположению индукции, $X \setminus Y$ можно разбить на $k - 1$ непустое множество точек, выпуклые оболочки которых пересекаются. Если добавить $Y$ к этому $k - 1$ множеству, то мы получим $k$ множеств, выпуклые оболочки которых пересекаются (так как выпуклая оболочка $Y$ содержит все точки из $X \setminus Y$). Если же $|Y| \geq 4k$, то рассмотрим два случая. Если все точки из $Y$ лежат на одной прямой, то и все точки из $X$ лежат на одной прямой. Проведем вдоль этой прямой ось координат и обозначим точки из $X$ через $A_1, A_2, \ldots, A_{|X|}$ по возрастанию координат. Так как $4k^2 > 2k$, то нам подходит разбиение: \[X = \{A_1, A_{|X|}\} \cup \{A_2, A_{|X|-1}\} \cup \ldots \cup \{A_{k-1}, A_{|X|-k+2}\} \cup \{A_k, A_{k+1}, \ldots, A_{|X|-k+1}\}.\] Иначе, точки $Y$ лежат на границе какого-то невырожденного выпуклого многоугольника. Обозначим точки из $Y$ в порядке обхода по часовой стрелке границы этого многоугольника через \[A_1, A_2, \ldots, A_k, B_k, B_{k-1}, \ldots, B_1, C_1, C_2, \ldots, C_k, D_k, D_{k-1}, \ldots, D_1, E_1, E_2, \ldots, E_{|Y| - 4k}.\] Пусть \[Z = \{A_k, B_k, C_k, D_k, E_1, \ldots, E_{|Y| - 4k}\} \cup (X \setminus Y).\] Докажем, что нам подходит следующее разбиение: \[X = \left(\bigcup_{i=1}^{k-1} \{A_i, B_i, C_i, D_i\}\right) \cup Z.\] Для этого достаточно доказать ключевое утверждение: выпуклые оболочки множеств \[\{A_1, B_1, C_1, D_1\}, \{A_2, B_2, C_2, D_2\}, \ldots, \{A_k, B_k, C_k, D_k\}.\] пересекаются. Через $f(M)$ будем обозначать выпуклую оболочку множества точек $M$. Пусть \[T \in A_1B_1 \cap A_kD_k,\] \[H_i = f(\{A_1, A_2, \ldots, A_i, B_i, B_{i-1}, \ldots, B_1, C_1, C_2, \ldots, C_i, D_i, D_{i-1}, \ldots, D_1\})\] и \[V_i = f(\{A_i, A_{i+1}, \ldots, A_k, B_k, B_{k-1}, \ldots, B_i, C_i, C_{i+1}, \ldots, C_k, D_k, D_{k-1}, \ldots, D_i\}).\] Тогда для любого $1 \leq i \leq k$ верно \[T \in A_1B_1 \subseteq H_i \ \text{и} \ T \in A_kD_k \subseteq V_i.\] Следовательно, \[T \in \bigcap_{i=1}^{k} (H_i \cap V_i) = \bigcap_{i=1}^{k} f(\{A_i, B_i, C_i, D_i\}),\] что и требовалось доказать.

Докажем, что $n=m\cdot 2^{m+1}$ подходит. Рассмотрим множество $S$ из $n$ точек. Очевидно, достаточно найти хотя бы $m$ непустых, попарно непересекающихся подмножества $S,$ выпуклые оболочки которых будут иметь общую точку.

Через $f(M)$ будем обозначать выпуклую оболочку множества точек $M.$

Шаг 1. “Сведем” задачу к выпуклому многоугольнику.

Пусть $V_1$ множество вершин $f(S)$ (берем только вершины этого выпуклого многоугольника). Аналогично определим $V_{i+1}$ для $f(S/ V_i).$ По итогу получим разбиение $S$ на непустые множества $V_1,…,V_k,$ причем

$$f(V_k)\subset f(V_{k-1}) \subset \ldots f(V_{1}).$$

Если $k \ge m,$ то требуемое разбиение найдено, иначе $\exists i: |V_i|>\dfrac{n}{m}=2^{m+1},$ выберем $X\subset V_i,$ что $|X|=2^{m+1}.$ Отметим, что точки этого множества образуют выпуклый многоугольник.

Шаг 2: Докажем индукцией по $m$, что $X$ можно разбить на $m$ множеств требуемым образом.

База для $m=1$ очевидна, для $m=2$ достаточно найти два отрезка (концы которых лежат в $S$) с общей точкой.

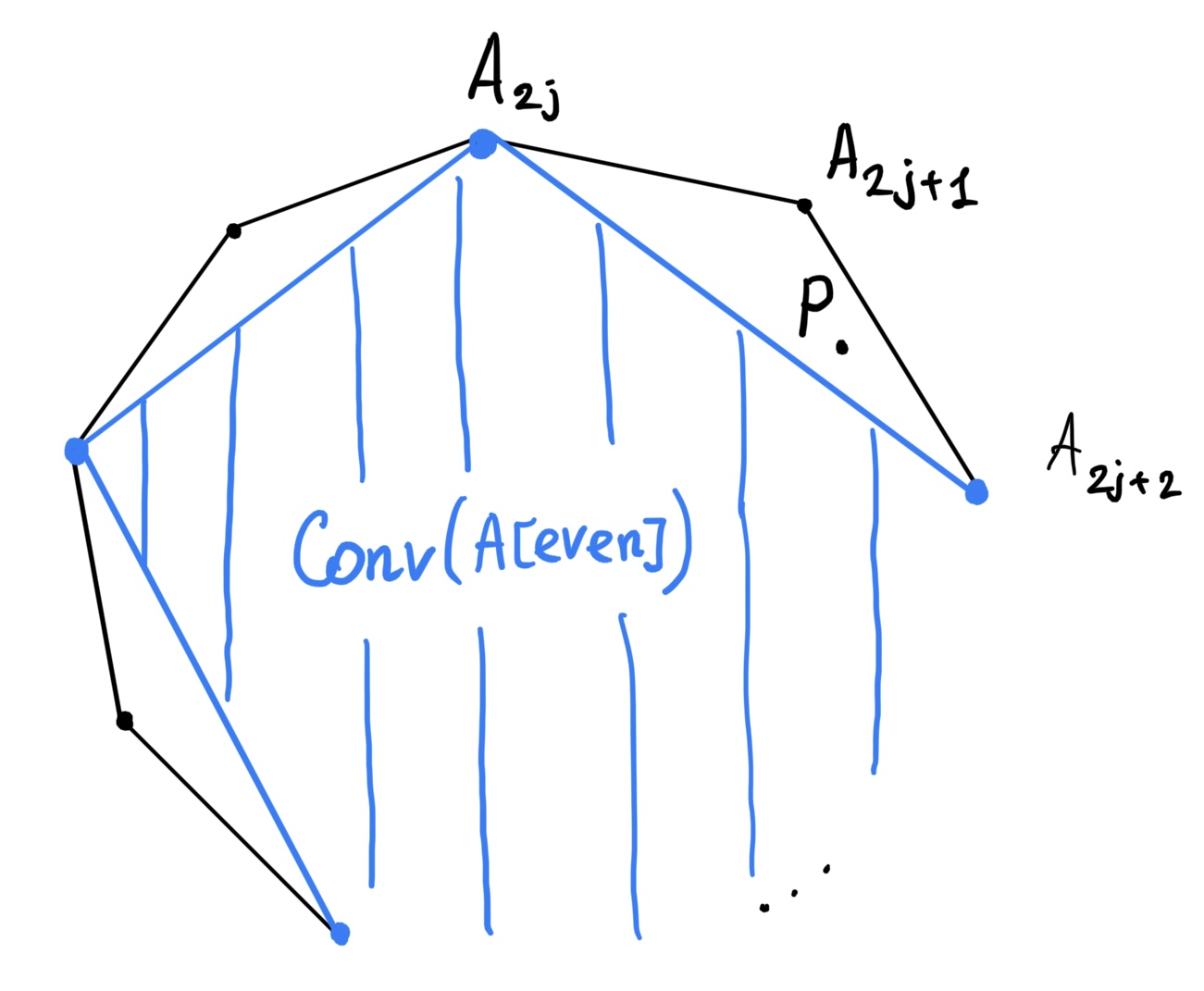
Допустим утверждение верно для $m-1\ge 2.$ Пусть $X$ образует многоугольник $A_1A_2\ldots A_{2^{m+1}}.$ Пусть $A[odd]=\{A_1,A_3,...,A_{2^{m+1}-1} \}, A[even]=\{ A_2,A_4,\ldots, A_{2^{m+1}} \}$

По предположению $A[odd]$ можно разбить на $m-1$ множеств, что $\exists P$ которая принадлежит выпуклой оболочке каждого $\Rightarrow P\in f (A[odd])\subset f(X).$

Достаточно доказать, что $P\in f ( A[even] ).$ Допустим обратное, тогда $P\in f (X/ A[even]) ,$ откуда $P\in f \{ (A_{2j},A_{2j+1},A_{2j+2} \} )$ для некоторого $j.$

В разбиений $A[odd]$ есть множество не содержащее $A_{2j+1},$ тогда $f$ от этого множества

$$\subset f (A[odd]/ \{A_{2j+1} \} )\subset f(X/ \{ A_{2j},A_{2j+1},A_{2j+2} \} ) \implies P\in f(X/ \{A_{2j},A_{2j+1},A_{2j+2} \} )$$

но точки из $f(X/ \{ A_{2j},A_{2j+1},A_{2j+2} \} )$ лежат по другую сторону от точки $P$ относительно прямой $A_{2j}A_{2j+2}.$ Противоречие.