Республиканская олимпиада по математике, 2021 год, 9 класс
Комментарий/решение:
Решение: Заметим, что $\angle TMQ=\angle TNQ$ и $\angle TCQ=\angle TBQ,$ значит $\triangle TMC \equiv \triangle TNB,$ следовательно
$$\dfrac{CM}{TM}=\dfrac{BN}{TN}$$
Построим точку $T_1$ так, чтобы $TMT_1N$ $-$ параллелограмм. Тогда заметим, что
$$\dfrac{PM}{T_1N}=\dfrac{CM}{TM}=\dfrac{BN}{TN}=\dfrac{PN}{T_1M}$$
$$\implies PM\cdot T_1M=PN\cdot T_1N\quad (\color{red}{1})$$
С другой стороны заметим, что
$$\angle MT_1N=\angle MTN = \angle MQN=\angle PCA + \angle PBD + \angle APD$$
$$=90+(\angle CPM+\angle BPN)=90+(90-\angle MPN)$$
$$\implies \angle MT_1N+\angle MPN = 180\implies \angle PMT_1+\angle PNT_1=180$$
$$\implies \sin \angle PMT_1=\sin \angle PNT_1\quad (\color{red}{2})$$
Из $(\color{red}{1})$ и $(\color{red}{2})$ получаем, что $S\left(\triangle PMT_1\right)=S\left(\triangle PNT_1\right),$ откуда прямая $PT_1$ проходит через середину $MN,$ а также мы знаем, что $TT_1$ проходит через эту середину, откуда следует требуемое.
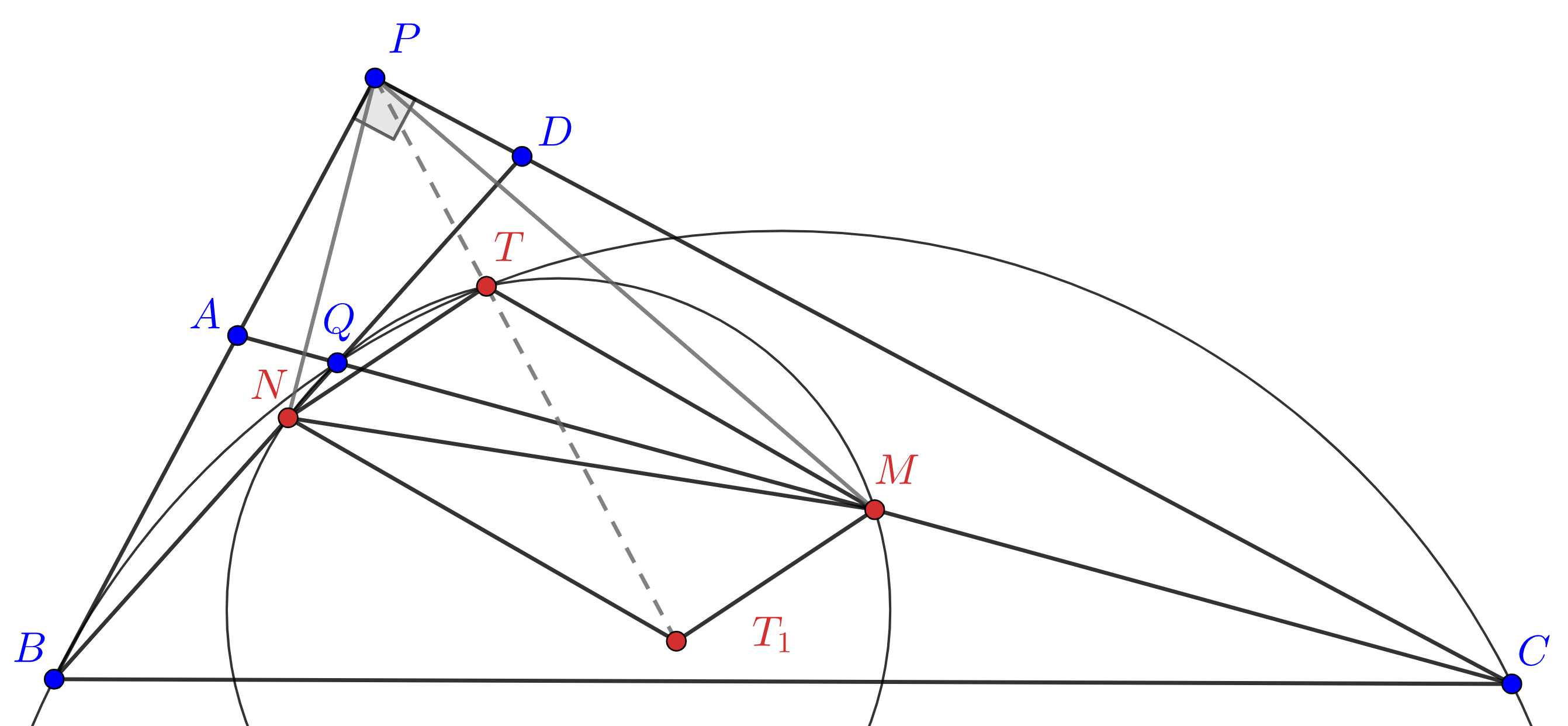
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.