Олимпиада имени Леонарда Эйлера 2022-2023 учебный год, II тур дистанционного этапа

$BM$ — медиана остроугольного треугольника $ABC$. Биссектриса угла $C$ пересекает прямую, проходящую через $A$ параллельно $BC$, в точке $X$. Оказалось, что $BM = MX$. Докажите, что $BC > AC$. ( С. Берлов )

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.    
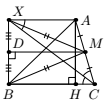
Решение. Проведем в треугольнике $ABC$ высоту $AH$. Утверждение задачи немедленно вытекает из равенства $AC = BH$, которое мы и будем доказывать. Проведем медиану $MD$ равнобедренного треугольника $BMX$. Она является средней линией трапеции (или параллелограмма) $AXBC$, и потому параллельна прямым $BC$ и $AX$. Так как эта медиана является в $BMX$ также и высотой, прямая $BX$ перпендикулярна ей, а потому и прямым $BC$ и $AX$. Следовательно, $BXAH$ — прямоугольник, откуда $BH = AX$. С другой стороны, $\angle CXA = \angle XCB = \angle XCA$, откуда $AC = AX = BH$, что нам и требовалось.