Республиканская олимпиада по математике, 2014 год, 9 класс


В выпуклом четырёхугольнике $ABCD$ справедливы следующие соотношения: $AB=BC$, $AD=BD$ и $\angle ADB = 2 \angle BDC$. Известно, что $\angle ACD = 100^\circ$. Найдите $\angle ADC$. ( М. Кунгожин )
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.     Пусть точка $C'$ симметрична точке $C$ относительно $BD$. Тогда $BC = BC'$ и $\angle CDB = \angle BDC'$. Откуда из условия задачи следует, что $\angle BDC' = \angle C'DA$, то есть $C'$ лежит на биссектрисе угла $BDA$.

Значит, $BC' = AC'$, откуда $ABC'$ — правильный треугольник. Точки $A$, $C$ и $C'$ лежат на одной окружности c радиусом $AB$ и центром в точке $B$. Поэтому $\angle ACC' = \angle ABC'/2 = 30^\circ$. Следовательно, $\angle C'CD = 70^\circ$, $\angle CDB = 20^\circ$ и $\angle CDA = 3 \angle CDB = 60^\circ$.

пред. Правка 4   3
2022-11-20 15:41:11.0 #

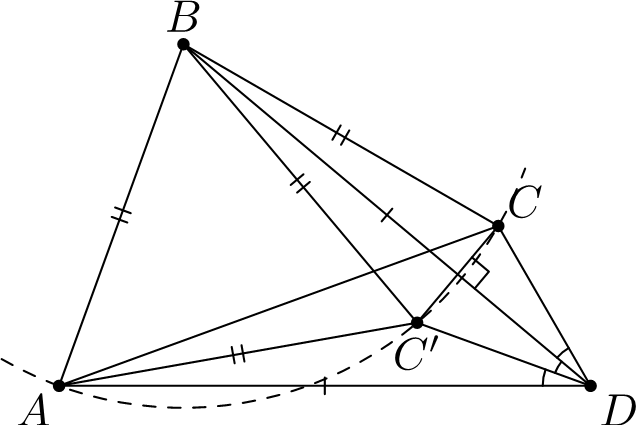
Пусть треугольник $DBE$ симметрично Треугольника $DBA$ относительно отрезка $DB$. тогда $DE=DB=DA$ и $BE=BC=BA$.

Пусть $\angle BDA=2\alpha, \angle CDB=\angle CDE=\alpha, \angle DBA=90-\alpha , \angle CAB=2\alpha+10, \angle CBA=160-4\alpha, \angle DBC=70-3\alpha, \angle EBC=2\alpha+20.$

Заметим, что Треугольник $CDE$ подобен на треугольника $CDB$ по двум одинаковым сторонам и равным углом $\alpha$.значит $EC=CB$ но также $EB=CB$ , из этого следует $ECB$ равносторонный треугольник. $\angle EBC=2\alpha+20=60 \Rightarrow \alpha=20, \angle ADC=3\alpha=60$.

AltynYerassyl
  0
2023-03-06 19:25:29.0 #

давайте обозначим $M$ через середину отрезка $AB$.Тогда скажем $\angle ADM$=

=$\angle MDB$=$\angle BDC$=$a$ тогда если $AM$=$MB$=$x$ $BC$=$2x$ а также

$x$=$y$$sin a$ если применить теорему синусов для $\triangle BMD$

также если применить теорему синусов для $\triangle BCD$ то можно получить что

$y$$sin a$=$2x$$sin (2a+110)$ из этого следует что $sin (2a+110)$*2=1 откуда $(2a+110)$=

=150 $a$=20 $3a$=60 откуда ответ 60

Sherkhan228