7-я международная Иранская олимпиада по геометрии, 2020 год, первая лига, 7-8 классы
Задача №1. Под сгибом многоугольного листа бумаги будем подразумевать проведение на этом листе отрезка и последующее перегибание листа по нему. Рассмотрим лист бумаги со следующим рисунком. Разрежем бумагу по границе закрашенной области, чтобы получился лист в форме многоугольника.
Начните с этого закрашенного многоугольника и, сделав не более чем 5 сгибов, получите из него лист в форме прямоугольника. В качестве решения нарисуйте линии сгибов и форму листа после каждого сгиба.
(Обратите внимание, что линии сгиба не обязаны совпадать с линиями сетки.)
комментарий/решение
Начните с этого закрашенного многоугольника и, сделав не более чем 5 сгибов, получите из него лист в форме прямоугольника. В качестве решения нарисуйте линии сгибов и форму листа после каждого сгиба.
(Обратите внимание, что линии сгиба не обязаны совпадать с линиями сетки.)
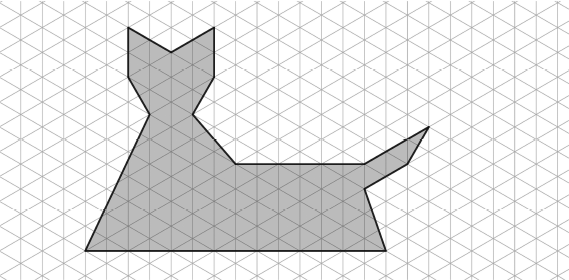
комментарий/решение
Задача №2. Дан параллелограмм $ABCD$ ($AB\neq BC$). Точки $E$ и $G$ на прямой $CD$ таковы, что $AC$ является биссектрисой каждого из углов $EAD$ и $BAG$. Прямая $BC$ пересекает $AE$ и $AG$ в точках $F$ и $H$ соответственно. Докажите, что прямая $FG$ проходит через середину отрезка $HE$.
комментарий/решение(1)
комментарий/решение(1)
Задача №3. Три равносторонних треугольника с длинами сторон $a$, $b$, $c$, расположенные, как показано на рисунке, имеют общую вершину и не имеют других общих точек. Определим длины $x$, $y$, $z$, как показано на рисунке. Докажите, что $3(x+y+z) > 2(a+b+c).$
комментарий/решение(11)
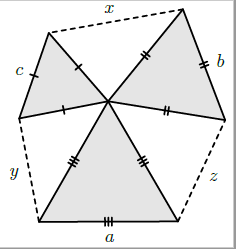
комментарий/решение(11)
Задача №4. Внутри треугольника $ABC$ выбрана произвольная точка $P$. Прямые $BP$ и $CP$ пересекают $AC$ и $AB$ в точках $E$ и $F$ соответственно. Точки $K$ и $L$ --- середины отрезков $BF$ и $CE$ соответственно. Прямые, проходящие через $L$ и $K$ параллельно $CF$ и $BE$, пересекают $BC$ в точках $S$ и $T$ соответственно. Обозначим через $M$ и $N$ точки, симметричные $S$ и $T$ относительно точек $L$ и $K$ соответственно. Докажите, что прямая $MN$ проходит через фиксированную точку, не зависящую от выбора точки $P$.
комментарий/решение(1)
комментарий/решение(1)
Задача №5. Скажем, что две вершины простого многоугольника видны друг из друга, либо если они соседние, либо если соединяющий их отрезок целиком лежит внутри многоугольника (за исключением двух концов, лежащих на границе). Найдите все натуральные $n$ такие, что существует простой многоугольник с $n$ вершинами, в котором каждая вершина видна ровно из четырёх других вершин.
(Простой многоугольник --- это несамопересекающийся многоугольник без дырок.)
комментарий/решение
(Простой многоугольник --- это несамопересекающийся многоугольник без дырок.)
комментарий/решение