9-я международная Иранская олимпиада по геометрии, 2022 год, вторая лига, 9-10 классы

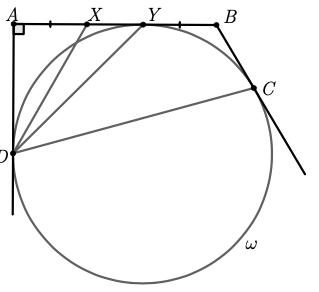
Задача №1. На рисунке ниже дано $AX = BY$. Докажите, что $\angle XDA = \angle CDY$.

Задача №2. Две окружности $\omega_1$ и $\omega_2$ одинакового радиуса пересекаются в точках $E$ и $X$. На $\omega_1$ и $\omega_2$ выбраны произвольные точки $C$ и $D$ соответственно. Прямые, проходящие через $E$ параллельно $XC$ и $XD$, пересекают $\omega_2$ и $\omega_1$ в точках $A$ и $B$ соответственно. Прямая $CD$ вторично пересекает $\omega_1$ и $\omega_2$ в точках $P$ и $Q$ соответственно. Докажите, что четырёхугольник $ABPQ$ вписанный.
комментарий/решение(1)

Задача №3. Пусть $O$ --- центр описанной окружности треугольника $ABC$. На сторонах $AC$ и $BC$ выбраны произвольные точки $M$ и $N$ соответственно. Точки $P$ и $Q$ лежат в той же полуплоскости относительно прямой $MN$, что и точка $C$, и удовлетворяют условию $\triangle CMN \sim \triangle PAN \sim \triangle QMB$ (подобия с указанным порядком вершин). Докажите, что $OP = OQ$.
комментарий/решение(1)

Задача №4. Будем называть два многоугольника $P$ и $Q$ совместимыми, если существует натуральное число $k$ такое, что $P$ можно разбить на $k$ равных многоугольников, подобных $Q$, а $Q$ можно разбить на $k$ равных многоугольников, подобных $P$. Докажите, что для любых двух чётных целых чисел $m, n \geq 4$ существует пара совместимых многоугольников, у которых $m$ и $n$ сторон.
(Многоугольник --- это часть плоскости, ограниченная замкнутой ломаной без самопересечений.)
комментарий/решение(1)

Задача №5. Четырёхугольник $ABCD$ вписан в окружность $\omega$ с центром в точке $O$. Диагонали $AC$ и $BD$ пересекаются в точке $P$. На отрезке $OP$ выбрана точка $Q$. Пусть $E$ и $F$ --- проекции $Q$ на прямые $AD$ и $BC$ соответственно. Точки $M$ и $N$ на описанной окружности треугольника $QEF$ таковы, что $QM \parallel AC$ и $QN \parallel BD$. Докажите, что прямые $ME$ и $NF$ пересекаются на серединном перпендикуляре к отрезку $CD$.
комментарий/решение(2)