Городская Жаутыковская олимпиада, 8 класс, 2007 год

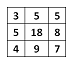
Задача №1. Во всех клетках таблицы $3\times 3$ первоначально записаны нули. Одним ходом разрешается прибавить ко всем четырем числам любого квадрата $2\times 2$ по единице. Можно ли после нескольких ходов получить нарисованную таблицу?

комментарий/решение(1)

Задача №2. Докажите, что квадратное уравнение $a{{x}^{2}}+bx+c=0$ имеет ровно один корень на интервале $\left( 0;1 \right)$, если числа $a$, $b$ и $c$ выражают длины сторон некоторого треугольника.
комментарий/решение

Задача №3. Группа туристов вышла из лагеря в 11 часов утра. В 11:30 один из туристов вспомнил, что он оставил в лагере компас, и побежал назад в лагерь. Взяв компас, он тут же побежал обратно и догнал группу в 13 часов. В котором часу он прибежал в лагерь.
комментарий/решение

Задача №4. Боковые стороны трапеции относятся как 1:2, а сумма углов при большем основании равна $120{}^\circ $. Найдите углы данной трапеции.
комментарий/решение(1)

Задача №5. Является ли число ${{3}^{22}}+5\cdot {{3}^{10}}+1$ простым?
комментарий/решение(1)

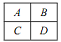
Задача №6. Прямоугольник разбит на четыре маленьких прямоугольника $A,B,C,D$. Среди чисел 3, 4, 5, 6, 7, 9, 11, 18 какие-то четыре выражают площади прямоугольников $A,B,C,D$. Найдите эту четверку чисел.

комментарий/решение(2)

Задача №7. На какое наименьшее натуральное число надо умножить произведение $1!\cdot 2!\cdot 3!\cdot \ldots \cdot 12!$, чтобы полученное произведение стало квадратом некоторого натурального числа? ($n!=1\cdot 2\cdot 3\cdot \ldots \cdot n$)
комментарий/решение(1)

Задача №8. Диагонали $AC$ и $BD$ четырехугольника $ABCD$ равны и пересекаются в точке $F$. Докажите, что прямая, соединяющая середины сторон $BC$ и $AD$, перпендикулярна биссектрисе угла $\angle CFD$.
комментарий/решение(5)