Городская Жаутыковская олимпиада, 9 класс, 2007 год
Задача №1. Решите систему уравнений: $\left\{ \begin{gathered}
3y - 2{x^2} = {x^2}y, \\
{\text{ }}y + 2x{\text{ }} = 3xy. \\
\end{gathered} \right.$
комментарий/решение(1)
комментарий/решение(1)
Задача №3. Каких треугольников с целочисленными сторонами больше: имеющих периметр 2007 или имеющих периметр 2010?
комментарий/решение
комментарий/решение
Задача №4. В четырехугольнике $ABCD$ стороны $AD$ и $CD$ равны, $\angle BCD=60{}^\circ $, $\angle BAC=30{}^\circ $. Докажите, что стороны $BC$ и $CD$ также равны.
комментарий/решение(1)
комментарий/решение(1)
Задача №5. Может ли число вида: а) $\underbrace{11...1}_{2007}2\underbrace{11...1}_{2007}$; б) $\underbrace{11...1}_{2008}2\underbrace{11...1}_{2008}$ быть простым?
комментарий/решение(1)
комментарий/решение(1)
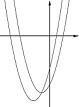
Задача №6. Могут ли изображенные на рисунке ниже параболы быть графиками функций $y={{x}^{2}}+px+q$ и $y={{x}^{2}}+qx+p$?
комментарий/решение
комментарий/решение
Задача №7. Пусть $a,b,c$ — вещественные числа. Докажите неравенство: $\dfrac{3}{2}({{a}^{4}}+{{b}^{4}}+{{c}^{4}})+24\ge 4{{a}^{2}}b+4{{b}^{2}}c+4{{c}^{2}}a.$
комментарий/решение(1)
комментарий/решение(1)
Задача №8. На стороне $AB$ треугольника $ABC$ отмечены точки $K$ и $L$ (точка $K$ лежит между точками $A$ и $L$). Известно, что $AK\cdot LB=AB\cdot KL$ и $\angle LCK=\angle LCB$. Докажите, что угол $ACL$ — прямой.
комментарий/решение(1)
комментарий/решение(1)