Математикадан «Туймаада» олимпиадасы. Жоғары лига. 2005 жыл
Есеп №1. $11\times 11$ кестесінің торларына $1$-ден $121$-ге дейінгі барлық натурал сандар жазылған. Дима әрбір жолдағы сандар көбейтіндісін есептеген, ал Саша әрбір бағандағы сандар көбейтіндісін есептеген. Олар $11$ санан тұратын бірдей жиындарды алуы мүмкін бе?
(
С. Берлов
)
комментарий/решение
комментарий/решение
Есеп №2. Халықаралық математикалық олимпиадаға Фатлияның командасының алты мүшесі $13$ үміткерден таңдалынып алынады. Іріктеу олимпиадасында үміткерлер ${{a}_{1}},{{a}_{2}},\ldots,{{a}_{13}}$ ұпай жинаған $\left( {{a}_{i}}\ne {{a}_{j}},i\ne j \right)$. Команда жетекшісі $6$ үміткерді алдын ала таңдап алып, енді командаға осы $6$ адам енгенін қалады. Осы мақсатпен ол $P(x)$ көпмүшелігін таңдап алып, әрбір үміткердің творчестволық деңгейін ${{c}_{i}}=P\left( {{a}_{i}} \right)$ формуласымен есептегісі келеді. Сонда $6$ үміткердің кез келгенінің творчестволық деңгейі қалған жетеуінің әрқайсысынан артық болатындай, $n$ дәрежесі артық емес қандай ең кіші $n$ үшін $P(x)$ көпмүшелігін алдын, іріктеп таңдап ала алады?
(
Ф. Петров,
К. Сухов
)
комментарий/решение
комментарий/решение
Есеп №3. Математикалық конгресті ұйымдастырушылар келген ғалымдарды қонақ үйге орналастырғанда байқағагндары: егер кез келген ғалымды біркісілік бөлмеге орналастырса, онда қалған ғалымдарды екікісілік бөлмелерге орналастырса, сонда әрбір бөлмедегі тұрғындар бір бірімен танысады. Дәлелдеу керек: конгресске қытысушы кез келген ғалым графтар теориясы бойынша дөңгелек үстел ұйымдастыра алады, ал оған оның өзінен басқа, тағыда жұп сан адам қатынаса алады және әрбір қатынасушы үстелдес екі көршісімен таныс болады.
(
С. Берлов,
С. Иванов
)
комментарий/решение
комментарий/решение
Есеп №4. $ABC$ үшбұрышы берілген. Үшбұрышқа іштейсырт сызылған шеңберлер $BC$, $CA$, $AB$ қабырғаларын сәйкес түрде ${{A}_{1}}$, ${{B}_{1}}$, ${{C}_{1}}$ нүктелерінде жанайды. $A{{A}_{1}}$, $B{{B}_{1}}$, $C{{C}_{1}}$ кесінділерінен үшбұрыш құрастыруға болатынын дәлелде.
(
Л. Емельянов
)
комментарий/решение(1)
комментарий/решение(1)
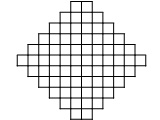
Есеп №5. Суретте кескінделген торлы тақтада барлық торды «соға» алатындай бірнеше ладьялар тұр (ладья өзі тұрған торды «соғады» деп есептеледі). Тақтада $11$- ден артық емес ладья қалдырып, сонда қалған ладьялардың барлық торларды бұрынғыдай «соғатындай» бірнеше ладьяны алып тастауға болатынын дәлелде.
комментарий/решение
комментарий/решение
Есеп №6. $n$ натурал саны және ${{x}_{0}}=\dfrac{{{a}_{0}}}{n},{{x}_{1}}=\dfrac{{{a}_{1}}}{n+1},{{x}_{2}}=\dfrac{{{a}_{2}}}{n+2},\ldots $ $\left( {{a}_{i}} < n+i \right)$ шектеусіз дұрыс бөлшектер тізбегі берілген ${{c}_{1}}{{x}_{1}}+{{c}_{2}}{{x}_{2}}+\ldots+{{c}_{k}}{{x}_{k}}=1$ болатындай $k$ натурал саны және бүтін сандары және ${{c}_{1}},{{c}_{2}},\ldots,{{c}_{k}}$ бүтін сандары бар болатынын дәлелдеу керек.
(
М. Дубашинский
)
комментарий/решение
комментарий/решение
Есеп №7. $I$ нүктесі $ABC$ үшбұрышына іштей сызылған шеңбер болсын. $B$ және $C$ төбелері арқылы өткен шеңбер $BI$ және $CI$ кесінділерін сәйкес түрде $P$ және $Q$ нүктелерінде қияды. $BP\cdot CQ=PI\cdot QI$ теңдігі орындалатыны белгілі. $PQI$ үшбұрышына сырттай сызылған шеңбер берілген үшбұрышқа сырттай сызылған шеңберді жанайтынын дәлелде.
(
С. Берлов
)
комментарий/решение
комментарий/решение
Есеп №8. ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=1$, шартын қанағаттандыратын кез келген оң $a,b,c$ сандары үшін
$\dfrac{a}{{{a}^{3}}+bc}+\dfrac{b}{{{b}^{3}}+ca}+\dfrac{c}{{{c}^{3}}+ab} > 3$ теңсіздігін дәлелде.
(
А. Храбров
)
комментарий/решение(5)
комментарий/решение(5)