1. Все олимпиады
  2. Математика
  3. Городские олимпиады
  4. Олимпиада им. Смагулова (6-7 классы)
  5. 1-я олимпиада им. Шалтая Смагулова (2016-2017 у.г.)
  6. 6 класс, 2 тур

1-я олимпиада им. Шалтая Смагулова, 6 класс, 2 тур, 2016 г.


Задача №1. Предприниматель покупает один товар по оптовой цене, равной 99 тенге. Для продажи этих товаров он сделал следующий маркетинговый ход: «Товар стоит $X$ тенге, но сегодня Вы сможете купить его со скидкой 70%». Известно, после этого объявления он продал весь товар за день. Чему равно $X$, если он с каждого товара получил прибыль ровно 99 тенге?
комментарий/решение(1)
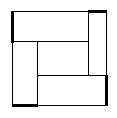
Задача №2. Квадрат со стороной 100 м разрезан на прямоугольники так, как показано на рисунке ниже (прямоугольники могут оказаться неравными). Сумма длин жирных отрезков равна 50 м. Найдите периметр внутреннего прямоугольника. Не забудьте обосновать ответ.


комментарий/решение(1)
Задача №3. Определите количество натуральных чисел от 1 до 2016, которые одновременно являются суммой двух последовательных натуральных чисел и суммой пяти последовательных натуральных чисел. (Например, $25 = 12 + 13 = 3 + 4 + 5 + 6 + 7$.)
комментарий/решение(2)
Задача №4. Можно ли в клетках квадрата 4х4 расставить числа от 1 до 16 по одному разу так, чтобы в каждом столбце и в каждой строке произведение чисел в клетках делилось на 16?
комментарий/решение(1)
Задача №5. Четыре человека обвиняются в грабеже. Известно, что
a) Если A виновен, то B также виновен;
b) Если B виновен, то либо C виновен, либо A не виновен;
c) Если D не виновен, то A виновен и C не виновен;
d) Если D виновен, то A также виновен.
Сколько человек из этих четырех виновны?
комментарий/решение(1)