1-я олимпиада им. Шалтая Смагулова, 7 класс, 2 тур, 2016 г.
Задача №1. Гани выбрал целое нечетное число между 1 и 99, причем оно не больше 90, не меньше 30, не является квадратом натурального числа, не является простым числом, не делится на 3, и его последняя цифра не равна 5. Какое число мог выбрать Гани (Укажите все возможные варианты, ответ обоснуйте)?
комментарий/решение(15)
комментарий/решение(15)
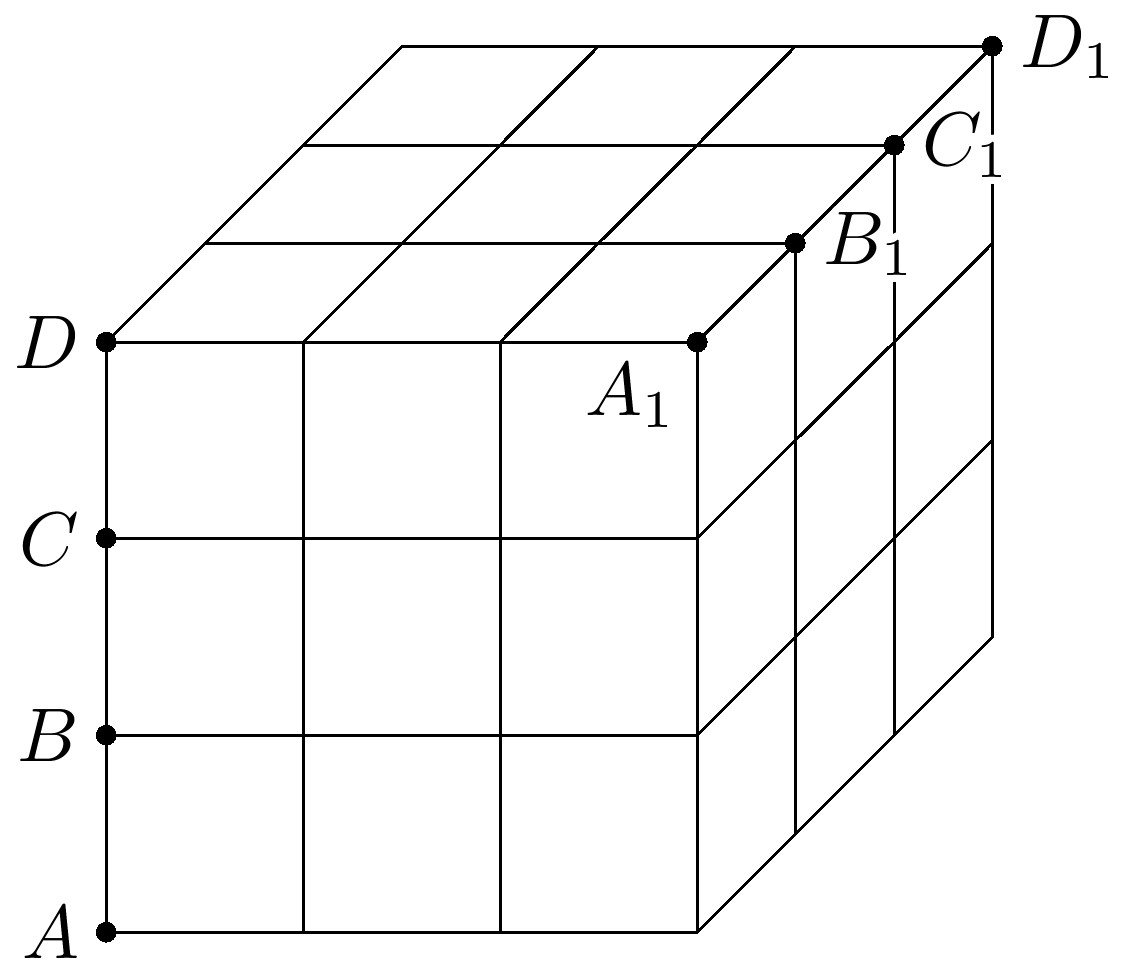
Задача №2. Куб состоит из 27 одинаковых кубиков, на ребрах которого отмечены точки $A,B,C,D,{{A}_{1}},{{B}_{1}},{{C}_{1}},{{D}_{1}}$ (см. рис. ниже). Четыре жука, имеющие одинаковые скорости, участвуют в необычном марафоне. У каждого есть свой старт и финиш: у первого это $A$ и ${{A}_{1}}$, у второго – $B$ и ${{B}_{1}}$, у третьего – $C$ и ${{C}_{1}}$ и, наконец, у четвертого – $D$ и ${{D}_{1}}$. При этом жуки могут перемещаться по поверхности куба по наикратчайшему пути. Если все жуки стартуют одновременно, то какой жук финиширует первым?
комментарий/решение(1)
комментарий/решение(1)
Задача №3. В треугольнике $ABC$ проведена высота $CH$. Известно, что биссектриса угла $A$ треугольника $ABC$ отсекает от угла $BCH$ равнобедренный треугольник с вершиной $C$. Докажите, что биссектриса угла $B$ треугольника $ABC$ также отсекает от угла $ACH$ равнобедренный треугольник с вершиной $C$.
комментарий/решение(1)
комментарий/решение(1)
Задача №4. У 10 девочек было по 10 конфет. Каждая девочка подарила несколько конфет другим (конфеты полученные в подарок, девочки оставляют себе). В результате у всех девочек оказалось разное количество конфет. Докажите, что какая-то из девочек подарила конфет не меньше, чем у нее их оказалось в конце.
комментарий/решение(1)
комментарий/решение(1)
Задача №5. Пятизначное число $A$ записывается только двойками и тройками, а шестизначное число $B$ – только четверками и тройками.
Али перемножил числа $A$ и $B$, получив в результате число, записываемое только двойками. Не ошибся ли он?
комментарий/решение(2)
комментарий/решение(2)