3-я международная Иранская олимпиада по геометрии, 2016 год, первая лига, 7-8 классы

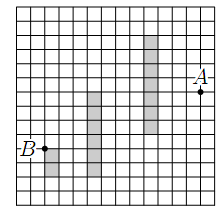
Задача №1. Али хочет добраться из точки

$A$ в точку

$B$ (см. рис.). По дороге ему нельзя заходить в закрашенные участки плоскости, а в остальные — можно. Путешествовать Али можно не только по линиям сетки, но и по всей плоскости. Помогите Али найти самый короткий путь из точки

$A$ в точку

$B$ . Просто нарисуйте путь и посчитайте его длину.

комментарий/решение(1)

Задача №2. Вокруг треугольника

$ABC$

$(AC>AB)$ описана окружность

$\omega$ . На стороне

$AC$ и на окружности

$\omega$ выбрали точки

$X$ и

$Y$ соответственно так, что

$CX=CY=AB$ . При этом точки

$A$ и

$Y$ лежат по разные стороны от прямой

$BC$ . Прямая

$XY$ пересекает окружность

$\omega$ второй раз в точке

$P$ . Докажите, что

$PB=PC$ .
комментарий/решение(1)

Задача №3. В выпуклом четырёхугольнике

$ABCD$ нет параллельных сторон. На каждой паре соседних сторон четырёхугольника

$ABCD$ построили параллелограммы. Докажите, что среди четырех новых точек ровно одна лежит внутри четырёхугольника

$ABCD$ .
комментарий/решение(1)

Задача №4. В прямоугольном треугольнике

$ABC$ (

$\angle A=90^{\circ}$ ) серединный перпендикуляр к гипотенузе

$BC$ пересекает прямую

$AC$ в точке

$K$ . Серединный перпендикуляр к отрезку

$BK$ пересекает прямую

$AB$ в точке

$L$ . Оказалось, что

$CL$ — биссектриса угла

$ACB$ . Найдите все возможные значения углов

$B$ и

$C$ .
комментарий/решение(1)

Задача №5. Известно, что в выпуклом четырёхугольнике

$ABCD$ :

$\angle ADC=135^{\circ}$ ,

$\angle ADB -\angle ABD=2\angle DAB=4\angle CBD$ ,

$BC=\sqrt{2} CD$ . Докажите, что

$AB=BC+AD$ .
комментарий/решение