Олимпиада Туймаада по математике. Младшая лига. 2019 год

Задача №1. В последовательности целых чисел

$a_1$ ,

$a_2$ ,

$ldots$ произведение

$a_1a_2$ отрицательно, а при

$n > 2$ для вычисления

$a_n$ среди всех пар

$(i, j)$ ,

$1\leq i < j < n$ , которые ранее не выбирались, выбирается одна пара

$(i, j)$ , для которой

$a_i+a_j$ имеет наименьшую абсолютную величину, и полагается

$a_n=a_i+a_j$ . Докажите, что

$a_i=0$ при некотором

$i$ . ( А. Голованов )
комментарий/решение(1)

Задача №2. Треугольник

$ABC$ , в котором

$AB < AC$ , вписан в окружность

$\omega$ . Окружности

$\gamma_1$ и

$\gamma_2$ касаются прямых

$AB$ и

$AC$ , а их центры лежат на окружности

$\omega$ . Докажите, что точка

$C$ лежит на общей внешней касательной к окружностям

$\gamma_1$ и

$\gamma_2$ . ( А. Кузнецов )
комментарий/решение(1)

Задача №3. План картинной галереи — клетчатая фигура, где каждая клетка — это зал, и из любой клетки можно дойти до любой другой, переходя в соседние по сторонам клетки. Смотритель, находясь в одном из залов, следит за всеми залами, в которые можно попасть из этой клетки одним ходом ладьи (не выходя за пределы галереи). Какое наименьшее число смотрителей потребуется, чтобы в любой галерее из

$n$ залов (

$n > 1$ ) все залы оказались под присмотром? ( H. Alpert, E. Roldan )
комментарий/решение

Задача №4. На Всероссийской олимпиаде разрешено награждать строго меньше

$45\%$ участников. В олимпиаде участвовало более 20 участников. После олимпиады Власти заявили, что результаты низкие, так как доля награждённых заметно отличается от

$45\%.$ Жюри ответило, что доля награждённых и так была максимально возможной на этой олимпиаде и даже на любой олимпиаде с меньшим числом участников. Тогда Власти приказали увеличить число участников на следующих олимпиадах с тем, чтобы доля награжденных стала хотя бы в два раза ближе к

$45\%.$ Докажите, что количество участников потребуется увеличить хотя бы вдвое. ( А. Голованов )
комментарий/решение

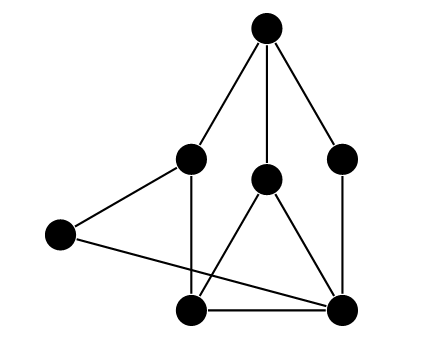
Задача №5. Можно ли нарисовать на плоскости граф, изображенный на рисунке, так, чтобы вершинам соответствовали различные точки плоскости, а все ребра изображались бы отрезками единичной длины? (Отрезки могут пересекаться в точках, не являющихся вершинами.)

( A. Globus, H. Parshall )
комментарий/решение(1)

Задача №6. Существуют ли такие 6 натуральных чисел, что наибольший общий делитель каждых двух из них — простое число, не превосходящее 26, и при этом каждое такое простое число является наибольшим общим делителем каких-то двух из этих шести чисел? ( А. Голованов )
комментарий/решение(2)

Задача №7. Окружность

$\omega$ касается сторон

$AB$ и

$BC$ треугольника

$ABC$ и пересекает сторону

$AC$ в точке

$K$ . Оказалось, что касательная к

$\omega$ в точке

$K$ симметрична прямой

$AC$ относительно прямой

$BK$ . Чему может быть равна разность

$AK-CK$ , если

$AB=9$ и

$BC=11$ ? ( С. Берлов )
комментарий/решение

Задача №8. Андрей, Боря, Витя и Гена играют на доске

$1000\times 1000$ . Ходят по очереди — сначала Андрей, потом Боря, затем Витя и наконец Гена, затем снова Андрей и т.д. Каждым ходом игрок должен закрасить еще незакрашенные клетки, образующие прямоугольник

$2\times 1$ ,

$1\times 2$ ,

$1\times 3$ или

$3\times 1$ . Проигрывает тот, кто не может сделать ход. Докажите, что какие-то трое ребят могут договориться и играть так, чтобы оставшийся заведомо проиграл. ( С. Берлов, Н. Власова )
комментарий/решение(1)